Thu 20 May 2010
I'm going to be out at Hac φ over the weekend cobbling together random bits and pieces of code, if you're going to be in the Philadelphia area, look us up!
In particular, I plan to spend my time working on my automatic differentiation library adding different directional traversals, and trying to combine them into a coherent framework.
Sat 15 May 2010
I've uploaded a package named heaps to Hackage that provides Brodal-Okasaki bootstrapped skew-binomial heaps in Haskell.
(more...)
Sat 15 May 2010
I've uploaded a package named rad to Hackage for handling reverse-mode automatic differentiation in Haskell.
(more...)
Thu 29 Apr 2010
I gave a talk last night at Boston Haskell on finger trees.
In particular I spent a lot of time focusing on how to derive the construction of Hinze and Paterson's 2-3 finger trees via an extended detour into a whole menagerie of tree types, and less on particular applications of the final resulting structure.
Tue 15 Sep 2009
I'll be giving a talk tomorrow, Wednesday, September 16th, 2009 at the Boston Haskell User Group in the MIT CSAIL Reading Room (on the 8th floor of the William H. Gates tower of the Stata center) about mixing Oleg's iteratees with parsec and monoids to build practical parallel parsers and to cheaply reparse after local modifications are made to source code.
Ravi is trying to organize some time before hand during which people can get together and work on Haskell projects, or spend some time learning Haskell, so its not all scary academic stuff.
The meeting is scheduled from 7-9pm, and an ever growing number of us have been wandering down to the Cambridge Brewing Company afterwards to hang out and talk.
If you are curious about Haskell, or even an expert, or just happen to be interested in parallel programming and find yourself in the area, come on by.
Tue 15 Sep 2009
Two concepts come up when talking about information retrieval in most standard documentation, Precision and Recall. Precision is a measure that tells you if your result set contains only results that are relevant to the query, and recall tells you if your result set contains everything that is relevant to the query.
The formula for classical precision is:
However, I would argue that the classical notion of Precision is flawed, in that it doesn't model anything we tend to care about. Rarely are we interested in binary classification, instead we want a ranked classification of relevance.
Sat 29 Aug 2009
I've been transcoding a lot of Haskell to Scheme lately and one of the things that I found myself needing was a macro for dealing with Currying of functions in a way that handles partial and over-application cleanly.
Thu 20 Aug 2009
I was asked to give two talks at the Boston Area Haskell User Group for this past Tuesday. The first was pitched at a more introductory level and the second was to go deeper into what I have been using monoids for lately.
The first talk covers an introduction to the mathematical notion of a monoid, introduces some of the features of my Haskell monoids library on hackage, and starts to motivate the use of monoidal parallel/incremental parsing, and the modification use of compression algorithms to recycle monoidal results.
The second talk covers a way to generate a locally-context sensitive parallel/incremental parser by modifying Iteratees to enable them to drive a Parsec 3 lexer, and then wrapping that in a monoid based on error productions in the grammar before recycling these techniques at a higher level to deal with parsing seemingly stateful structures, such as Haskell layout.
Due to a late start, I was unable to give the second talk. However, I did give a quick run through to a few die-hards who stayed late and came to the Cambridge Brewing Company afterwards. As I promised some people that I would post the slides after the talk, here they are.
The current plan is to possibly give the second talk in full at either the September or October Boston Haskell User Group sessions, depending on scheduling and availability.
[ Iteratee.hs ]
Sat 15 Aug 2009
I have updated the reflection package on hackage to use an idea for avoiding dummy arguments posted to the Haskell cafe mailing list by Bertram Felgenhauer, which adapts nicely to the case of handling Reflection. The reflection package implements the ideas from the Functional Pearl: Implicit Configurations paper by Oleg Kiselyov and Chung-chieh Shan.
Now, you no longer need to use big scary undefineds throughout your code and can instead program with implicit configurations more naturally, using Applicative and Monad sugar.
Fri 31 Jul 2009
Some people have requested my slides from the short talk I gave about monoids and monoidal parsing at Hac Phi. So, here they are.
There will be more to come at the next Boston Haskell User Group in August, where it looks like I'll be giving two short talks covering monoids. I may use the monoidal parsing engine from Kata as an example for the advanced talk if I have time and will start to cover parsing larger classes of grammars in general (regular languages, CFGs/TIGs, TAGs, PEGs, LALR, attribute-grammars, etc.)
Thu 11 Jun 2009
About a year back I posted a field guide of recursion schemes on this blog and then lost it a few months later when I lost a couple of months of blog entries to a crash. I recently recovered the table of recursion schemes from the original post thanks to Google Reader's long memory and the help of Jeff Cutsinger.
The following recursion schemes can be found in category-extras, along with variations on the underlying themes, so this should work as a punch-list.
| Folds | ||
|---|---|---|
| Scheme | Code | Description |
| catamorphism† | Cata | tears down a structure level by level |
| paramorphism*† | Para | tears down a structure with primitive recursion |
| zygomorphism*† | Zygo | tears down a structure with the aid of a helper function |
| histomorphism† | Histo | tears down a structure with the aid of the previous answers it has given. |
| prepromorphism*† | Prepro | tears down a structure after repeatedly applying a natural transformation |
| Unfolds | ||
| Scheme | Code | Description |
| anamorphism† | Ana | builds up a structure level by level |
| apomorphism*† | Apo | builds up a structure opting to return a single level or an entire branch at each point |
| futumorphism† | Futu | builds up a structure multiple levels at a time |
| postpromorphism*† | Postpro | builds up a structure and repeatedly transforms it with a natural transformation |
| Refolds | ||
| Scheme | Code | Description |
| hylomorphism† | Hylo | builds up and tears down a virtual structure |
| chronomorphism† | Chrono | builds up a virtual structure with a futumorphism and tears it down with a histomorphism |
| synchromorphism | Synchro | a high level transformation between data structures using a third data structure to queue intermediate results |
| exomorphism | Exo | a high level transformation between data structures from a trialgebra to a bialgebraga |
| metamorphism | Erwig | a hylomorphism expressed in terms of bialgebras |
| metamorphism | Gibbons | A fold followed by an unfold; change of representation |
| dynamorphism† | Dyna | builds up a virtual structure with an anamorphism and tears it down with a histomorphism |
| Elgot algebra | Elgot | builds up a structure and tears it down but may shortcircuit the process during construction |
| Elgot coalgebra | Elgot | builds up a structure and tears it down but may shortcircuit the process during deconstruction |
* This gives rise to a family of related recursion schemes, modeled in category-extras with distributive law combinators
† The scheme can be generalized to accept one or more F-distributive (co)monads.
Tue 31 Mar 2009
Recently, Sean Leather took up the idea of incremental folds. [1] [2]. At the end of his first article on the topic he made a comment on how this was a useful design pattern and sagely noted the advice of Jeremy Gibbons that design patterns are more effective as programs, while complaining of cut and paste coding issues.
The following attempts to address these concerns.
Thu 4 Dec 2008
Last night, Chung-Chieh Shan posted an example of a pointed-set monad on his blog, which happens to be isomorphic to a non-empty stream monad with a different emphasis.
But, I thought I should point out that the pointed set that he posted also has a comonadic structure, which may be exploited since it is just a variation on the "zipper comonad," a structure that is perhaps more correctly called a "pointing comonad."
Sat 8 Nov 2008
To those that have asked, I'm still alive.
I had to restore the blog database from a backup and so I lost a few posts, including the index for the various recursion schemes entries. Fortunately, before that happened I had replicated the catamorphism post as a knol.
Should I find myself with a copious glut of free time, I shall happily re-scribe and finish the rest, but I've been very busy.
Thu 5 Jun 2008
As you may recall, every functor in Haskell is strong, in the sense that if you provided an instance of Monad for that functor the following definition would satisfy the requirements mentioned here:
strength :: Functor f => a -> f b -> f (a,b) strength = fmap . (,)
In an earlier post about the cofree comonad and the expression problem, I used a typeclass defining a form of duality that enables you to let two functors annihilate each other, letting one select the path whenever the other offered up multiple options. To have a shared set of conventions with the material in Zipping and Unzipping Functors, I have since remodeled that class slightly:
Thu 5 Jun 2008
I've had a few people ask me questions about Adjunctions since my recent post and a request for some more introductory material, so I figured I would take a couple of short posts to tie Adjunctions to some other concepts.
Representable Functors
A covariant functor 
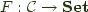is said to be representable by an object 
if it is naturally isomorphic to 
.
We can translate that into Haskell, letting 
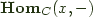play the role of 
with:
Tue 3 Jun 2008
This post is a bit of a departure from my recent norm. It contains no category theory whatsoever. None. I promise.
Now that I've bored away the math folks, I'll point out that this also isn't a guide to better horticulture. Great, there goes the rest of you.
Instead, I want to talk about Bloom filters, Bloom joins for distributed databases and some novel extensions to them that let you trade in resources that we have in abundance for ones that are scarce, which I've been using for the last few months and which I have never before seen before in print. Primarily because I guess they have little to do with the strengths of Bloom filters.
Mon 26 May 2008
Grant B. asked me to post the derivation for the right and left Kan extension formula used in previous Kan Extension posts (1,2). For that we can turn to the definition of Kan extensions in terms of ends, but first we need to take a couple of steps back to find a way to represent (co)ends in Haskell.
Thu 22 May 2008
I want to spend some more time talking about Kan extensions, composition of Kan extensions, and the relationship between a monad and the monad generated by a monad.
But first, I want to take a moment to recall adjunctions and show how they relate to some standard (co)monads, before tying them back to Kan extensions.
Adjunctions 101
An adjunction between categories 
and 
consists of a pair of functors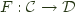 
, and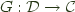 
and a natural isomorphism: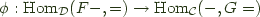
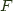We call 
the left adjoint functor, and 
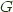the right adjoint functor and 
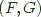an adjoint pair, and write this relationship as 
Tue 20 May 2008
I think I may spend a post or two talking about Kan extensions.
They appear to be black magic to Haskell programmers, but as Saunders Mac Lane said in Categories for the Working Mathematician:
All concepts are Kan extensions.
So what is a Kan extension? They come in two forms: right- and left- Kan extensions.
First I'll talk about right Kan extensions, since Haskell programmers have a better intuition for them.
