Tue 3 Jun 2008
This post is a bit of a departure from my recent norm. It contains no category theory whatsoever. None. I promise.
Now that I've bored away the math folks, I'll point out that this also isn't a guide to better horticulture. Great, there goes the rest of you.
Instead, I want to talk about Bloom filters, Bloom joins for distributed databases and some novel extensions to them that let you trade in resources that we have in abundance for ones that are scarce, which I've been using for the last few months and which I have never before seen before in print. Primarily because I guess they have little to do with the strengths of Bloom filters.
For practical purposes you will need to use a counted or spectral Bloom filter for the purposes of the structure mentioned below. However, as these introduce nothing novel, and simply muddle the exposition, I'll ignore counting and spectral Blooms for now.
Bloom Filters
Ok, so what is a Bloom filter? Bloom filters date back to 1970. A simple Bloom filter is a novel data structure for approximating membership in a set, yielding only false positives. A filter consists of an m-bit array and k distinct hash functions. To add an element to the filter you run it through each of the k hash functions and setting the appropriate bits. A value is considered to be a member of the set if you hash it through each of the k functions and each of the target bits is set. It is easy to see that this can only result in a false positive, but its also easy to see that you need to set the size of the array before you start adding elements to it, and that you need to balance the number of hash functions to the overall desired precision of your filter. In general you want to have about half of the bits set in the resulting array to maximize your information density -- a fact which can be derived with elementary calculus. From which you can figure out that you get optimal results when 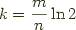 .
.
We can readily approximate k distinct hashing functions by using a single one-way hashing function and carving it up into a number of hashing functions that consist of the right number of bits each. A simpler approach due to Kirsch and Mitzenmacher is to sacrifice the independence of the hash functions without particularly adversely affecting the properties of the filter.
The nice thing about a Bloom filter is that the parameters m and k can be varied to tune space requirements and precision.
Improving Locality
One common way to improve the locality of reference for excessively large Bloom filters is to break up the structure into two tiers. You have an upper tier in which you use a single hash function to bin the data, then within the bin you placed the data you run the remaining k-1 hash functions. This can result in a 'lumpier' distribution of data, but generally improves performance because if you exceed working memory, this model can typically page in a single page from disk to handle the k-1 writes. When you figure that it is common to use between several hashing functions with a bloom filter this can result in a several-fold performance improvement as the data set grows and you become IO bound. As a result of being primarily to optimize IO you typically want to have a bin size that corresponds with your block or page size.
As an admittedly completely unintelligible aside, I am particularly fond of 8k bins for a simple Bloom filter, because they nicely consume 16 bits of hash evenly, and 4k bins, when used with 4 bit counting Blooms, page in and out efficiently and compress nicely with an arithmetic/exponentiated Huffman encoding into near even multiples of the ethernet packet MTU when you tune the ratio of set bits carefully, I've found this to be beneficial for tweaking real world performance.
Bloom Joins
Given a pair of bloom filters that share a given size m and which use the same k hash functions. You can take their intersection (or union) quite efficiently with bitwise and (or or). This is a well known technique for dealing with distributed database joins when you have data distributed across multiple servers joining against data distributed across other servers. In general, you are only interested in transmitting the data that exists on both sides of the join.
(You can technically free yourself from the requirement that both sides agree on the number of hash functions if you are willing to accept more false positives and you test for membership in the result set using just the hash functions contained in both Blooms. The easiest way to do this is to just agree on an order in which hash functions will be used, which comes for free from the Kirsch/Mitzenmacher approach mentioned above.)
The good
The nice thing about a standard Bloom join is that you can send the Bloom filter over the network quite cheaply in comparison to the data, and with the addition of counting Bloom filter tricks it can be used to calculate approximately the size of the result set. This allows you to use it to load level MapReduce style workloads effectively by estimating the size of intermediate results quite accurately before you send everything over the network to be aggregated.
The bad
One problem with this model is that you have to know the size of your data set up front in order to calculate an ideal m for a desired precision level. Moreover both sides of the join have to agree on this figure m before calculating the join.
Now, the main goal of a Bloom join is to conserve an scarce resource (network bandwith) by exchanging cheaper, more plentiful resources (local CPU utilization, and disk IO). In that respect it serves adequately, but we can do better if our goal is more or less purely to optimize network bandwidth. Lets carry that a bit further.
Linear Hash Tables
To address the limitation that you have to know the size of the bloom a priori, we'll turn to another data structure, the linear hash table. Linear hash tables were designed by Witold Litwin back in 1980 to provide an expandable hash table without a huge stairstep in the cost function whenever you hit a power of two in size. The basic idea of a linear hash table is that you grow the table gradually, by splitting one bucket at a time and using the least significant bits of your hash function.
For sake of variety, I've included a C# 3.5 implementation here:
[SortedLinearHashTable.cs]
[SinglyLinkedList.cs]
[PreparedEqualityComparer.cs]
[PreparedEqualityComparerTypeProxyAttribute.cs]
For my regular audience, an implementation in Haskell using STM — incidentally was the first piece of Haskell I ever wrote — designed for read-mostly use can be found here:
A Linear Bloom Filter
Now, we can look at the bi-level structure we introduced above for dealing with improved cache locality and note that we could go in a different direction and treat the upper level as a linear hash table, instead of a simple hash function! This requires that we keep not only the Bloom but also the member list (or at least their hashes). We can optimize this slightly by computing the Bloom of the member list for each page lazily. This costs us quite a bit of storage relative to a traditional Bloom filter, but we can transmit the Bloom of the resulting set over the network more cheaply than we can transmit a linear hash table and it isn't appreciably more expensive locally than a linear hash table due to only lazily constructing the Blooms.
This mechanism gives rise to an actual tree of pages based on the unfolding of the linear hash table in the resulting hierarchical bloom if you choose to represent the interior of the tree.
Again, this isn't a win for all scenarios, but if you are intending to transmit the resulting set over the network, and don't know its size a priori, the combination of properties from the linear hash table and the bloomed pages leads to some interesting options.
Linear Bloom Origami
Now that we have an expandable hash in our top level, we finally have the machinery to deal with how to perform a join between two linear bloom filters of different size. The model is actually quite simple. We can fold the larger bloom up by oring together the leaves that were split by the linear hash table in the larger bloom until we have the same number of pages and then perform a standard Bloom join. This frees us from the tyranny of having to have both sides of the join guess in advance a shared number of buckets to use to perform the join.
As an aside, an interesting thought experiment is to go one step further and use a full-fledged sorted linear hash table for the extra cost of sorting the chains, but this doesn't seem to be useful in practice.
Mipmapping Blooms
If we are willing to pay an 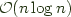 cost in terms of the data set size cost in terms of CPU utilization and memory bandwidth we can gain some further performance in terms of network utilization through encoding a set of "mipmaps" for our filters.
cost in terms of the data set size cost in terms of CPU utilization and memory bandwidth we can gain some further performance in terms of network utilization through encoding a set of "mipmaps" for our filters.
Basically the idea is to fold up the tree by oring together the pages into an admissible Bloom of the dataset. Then you encode the splitting of each bit that was set in the Bloom using conditional probabilities. This can be transmitted near optimally using arithmetic encoding or exponentiated Huffman.
If a bit is set in the parent Bloom, then at least one of the two bits will be set in the child Blooms; if no bit is set in the parent Bloom, then no bit can be set in the child Blooms. The probability of each bit being set in each child is for all practical intents and purposes independent and can reasonably be modeled as a function of the expected number of set bits. (This is ever-so-slightly suboptimal if the overall number of values is known). You can determine exact values for the weights of each of the three cases using conditional probabilities and then use an arithmetic compressor, or exponentiate the alphabet for a Huffman compressor — this is otherwise near worst-case for Huffman, since you have two possibilities both just shy of 50% and one much smaller probability. Nicely the regular structure of the exponentiated alphabet is very regular and can be represented efficiently. With careful choice of page size (or bit density within a page) you can transmit the initial page cheaply, and then pack multiple pages into subsequent packets.
Since we can determine the relevance of portions of the tree based on partial information this may allow you to avoid transmitting some branches of the tree. More interestingly we can use it to figure out approximately the size of the join set from the first few pages transmitted and to gain gradual refinements as both sides of the join supply more information.
If you wanted to optimize strictly for network bandwidth and were willing to accept additional latency you could prune branches of the tree after it was clear that the intersection was empty and so no further resolution was required, but in my experience this optimization doesn't seem to be worth the effort.
Incremental Update
Interestingly if you have already shared a Linear Bloom and need to update your copy it admits a cheap network representation using the same arithmetic/exponentiated Huffman encoding trick mentioned earlier. You lose the ability to ignore all unset bits in the dataset because extending the set of known values will in all likelihood set new bits, but as you add members you can transmit splits using the same mechanism used above, and you have the actual member set needed to populate the child pages accurately.
Interestingly it is the ability to mipmap the intermediate results that sometimes makes it worth dealing with a suboptimal choice of density for the overall Bloom filter, because it only affects the cost on either end of the network, it doesn't affect the network transmission costs all that adversely and more sparse population early in the tree can allow you to have a less oversaturated tree near the root, allowing earlier pruning of branches - I have yet to take this from an art to a science.
Conclusion
I had intended to explain things in more detail and delve into the asymptotic behavior of hierarchical and linear Blooms, but various people have been hammering me to just post this already, so here it is.
So to recap, we took a normal (or counted or spectral) Bloom filter, crossbred it with Litwin's linear hash table and found that the mutant offspring is an approximation of a set that is better suited to sharing over the network than either structure alone, with a memory usage profile similar to that of a linear hash table. Interestingly as a side effect you can go one step further and allow for transmission of a requested subset of the exact hashes present in which case we've really only used the Blooms to provide partial information about the underlying linear hash table, which can aid in the subsequent join process.
And yes, they are probably better named something like Bloomed linear hash tables, but that doesn't roll off the tongue.
If there is enough interest and I don't get dragged into other things, I might see about packaging up and genericizing some code that I had lying around intended for production use into a more general purpose library for Linear Bloom Filters.

June 4th, 2008 at 12:51 am
This is me expressing interest in both the general purpose Linear Bloom Filter library, and the asymptotic behavior.
June 4th, 2008 at 2:01 am
Bah. You don’t count. You already have access to the original library. =)
June 4th, 2008 at 9:28 pm
With all that talk of bloom filters and even a few mentions of mipmaps I thought you would have thrown in a few screenshots. Ha.
June 4th, 2008 at 10:30 pm
Hah! Sorry Mo.
Unfortunately nothing I do these days makes for great screenshots. Maybe I should go back to voxels and stabbing line problems. ;)
I suppose you could Bloom a scene’s PVS or something, but its not all that useful for its primary purpose because then you wouldn’t be able to extract the member cells. Hrmm. That said, I guess it could be used for a quick, “is this model that overlaps these cells probably visible?” tester.
I almost referred to the hierarchical representation as a kind of Haar wavelet encoding, but I figured that would cause the last person in the audience to tune me out.
P.S. The alpaca on your page still refers to blabberize as ‘the technology of 2007′ ;)
June 5th, 2008 at 8:28 pm
[...] The Comonad.Reader » Linear Bloom Filters (tags: algorithm algorithms article data math research programming) [...]
August 5th, 2008 at 2:02 pm
Your article was well-written and is very interesting. I was really geeking out on it and I am not even a mathematician. I think the article would have made my ex-girlfriend hot.
Anyway, all jokes aside, I am surprised to find Bloom Filter usage very sparse within the general software industry (I am a consultant-of-one running my own company but have large clients in the Fortune 100, start-ups, etc).
The case you presented here for being able to efficiently serialize the filter has notable use in web-application farm environments where sessions and other state table information must be migrated between servers (depending on session management strategy employed). Indeed one challenge I am considering is somehow managing some Bloom Filter construct across a RAIN architecture without sacrificing the small memory footprint and performance advantages that Blooms provide.
Thanks again.
March 8th, 2009 at 12:52 pm
Edward, are you aware of any specific paper discussing theoretical properties of the two-tier Bloom filter architecture? I am specifically interested in a comparison of false-positive rates of two-tier filters and standard filters.
March 8th, 2009 at 6:00 pm
Christian you might want to check out:
http://algo2.iti.uni-karlsruhe.de/singler/publications/cacheefficientbloomfilters-wea2007.pdf
Although they concern themselves with clustering within a single cache line, the idea of clustering within a page follows similarly.
IIRC they take up like ~32% extra space to get the same precision, but they use VERY small buckets of the same size as a cache line. So that should give you an upper bound for space comparison that you can back into a false positive rate comparison.
March 9th, 2009 at 6:07 am
Thanks, Edward. If I get this right, the larger the single buckets, the closer the two-tier variant performs to the standard variant (in sense of the false-positive rate for a total length of m)?
March 10th, 2009 at 4:43 pm
Yes.
If you have p bits of hash function available to you, and the top tier consumes q of them, then at one extreme q = 0, and you have all p bits available for use within the one bucket, cutting p up into k different hash functions yields the traditional Bloom filter.
In the other extreme you have q = p, and you have the efficacy of a bloom table/bit-hash with one hash function.
In the middle the false positive rate lies somewhere in between, but you only have to deal with data points within a single bucket to answer the query, so you can typically save a factor of k in paging or cache-thrashing costs.
April 7th, 2009 at 7:41 pm
Ed,
I know you and some of your readers love Haskell so I thought I would share this funny (but real) programming language I just read about:
http://compsoc.dur.ac.uk/whitespace/index.php
September 23rd, 2022 at 3:27 am
Viagra vs viagra https://500px.com/p/skulogovid/?view=groups...
Cheers. I like it….
September 23rd, 2022 at 7:34 am
Viagra rezeptfrei https://500px.com/p/bersavahi/?view=groups...
Nicely put, Cheers!…
September 24th, 2022 at 12:37 am
online canadian pharmacy https://reallygoodemails.com/canadianpharmaceuticalsonlineusa...
You actually reported that fantastically!…
September 24th, 2022 at 4:17 am
Viagra pills https://www.provenexpert.com/canadian-pharmaceuticals-online-usa/...
With thanks. Ample write ups.
…
September 24th, 2022 at 9:24 am
Viagra prices https://sanangelolive.com/members/pharmaceuticals...
Awesome write ups. With thanks!…
September 26th, 2022 at 8:18 am
Interactions for viagra https://melaninterest.com/user/canadian-pharmaceuticals-online/?view=likes...
You actually suggested this terrifically….
September 26th, 2022 at 12:20 pm
canadian pharmacy online https://haikudeck.com/canadian-pharmaceuticals-online-personal-presentation-827506e003...
Really quite a lot of useful information!…
September 26th, 2022 at 4:30 pm
Tadalafil 20 mg https://buyersguide.americanbar.org/profile/420642/0...
With thanks. I like this!…
September 27th, 2022 at 6:10 am
Viagra generika https://slides.com/canadianpharmaceuticalsonline...
With thanks! A lot of knowledge.
…
September 27th, 2022 at 9:47 am
stromectol france https://challonge.com/esapenti...
You have made your point quite effectively!….
September 27th, 2022 at 2:16 pm
Viagra purchasing https://challonge.com/gotsembpertvil...
Very good posts. Thanks a lot….
September 28th, 2022 at 4:03 am
Viagra alternative https://challonge.com/citlitigolf...
Very good forum posts. Kudos!…
September 28th, 2022 at 7:37 am
stromectol sale https://order-stromectol-over-the-counter.estranky.cz/clanky/order-stromectol-over-the-counter.html...
Great forum posts. Thanks a lot!…
September 28th, 2022 at 2:03 pm
Viagra vs viagra https://soncheebarxu.estranky.cz/clanky/stromectol-for-head-lice.html...
Thanks a lot! Quite a lot of stuff!
…
September 29th, 2022 at 3:36 am
How does viagra work https://lehyriwor.estranky.sk/clanky/stromectol-cream.html...
Appreciate it, Numerous forum posts.
…
September 29th, 2022 at 7:23 am
Viagra pills https://dsdgbvda.zombeek.cz/...
Amazing quite a lot of excellent facts!…
September 29th, 2022 at 1:48 pm
Tadalafil 5mg https://inflavnena.zombeek.cz/...
With thanks! An abundance of material!
…
September 30th, 2022 at 8:06 am
Generic viagra https://www.myscrsdirectory.com/profile/421708/0...
Very good content. Many thanks!…
September 30th, 2022 at 3:15 pm
Tadalafil https://supplier.ihrsa.org/profile/421717/0...
Nicely put, Many thanks….
October 1st, 2022 at 5:37 am
Viagra cost https://wefbuyersguide.wef.org/profile/421914/0...
Terrific knowledge. Thanks a lot….
October 1st, 2022 at 9:38 am
Tadalafil tablets https://legalmarketplace.alanet.org/profile/421920/0...
Nicely put, Thanks….
October 2nd, 2022 at 3:15 am
Tadalafil https://moaamein.nacda.com/profile/422018/0...
You revealed it fantastically!…
October 2nd, 2022 at 7:42 am
Viagra daily https://www.audiologysolutionsnetwork.org/profile/422019/0...
Wow plenty of superb information!…
October 2nd, 2022 at 11:00 am
Viagra reviews https://network.myscrs.org/profile/422020/0...
You made your stand very effectively!!…
October 3rd, 2022 at 4:45 am
Cheap viagra https://sanangelolive.com/members/canadianpharmaceuticalsonlineusa...
You actually revealed that exceptionally well….
October 3rd, 2022 at 8:09 am
Viagra kaufen https://sanangelolive.com/members/girsagerea...
Seriously plenty of good knowledge!…
October 4th, 2022 at 6:49 am
Viagra bula https://www.ecosia.org/search?q=“My Canadian Pharmacy – Extensive Assortment of Medications – 2022″…
You expressed this adequately….
October 4th, 2022 at 10:33 am
Cheap viagra https://www.mojomarketplace.com/user/Canadianpharmaceuticalsonline-EkugcJDMYH...
Amazing tons of very good material….
October 4th, 2022 at 2:57 pm
Viagra tablets https://seedandspark.com/user/canadian-pharmaceuticals-online...
Kudos. Valuable information….
October 5th, 2022 at 2:51 am
Viagra online https://www.giantbomb.com/profile/canadapharmacy/blog/canadian-pharmaceuticals-online/265652/...
Perfectly spoken really! ….
October 5th, 2022 at 11:50 am
legitimate canadian mail order pharmacies https://feeds.feedburner.com/bing/Canadian-pharmaceuticals-online...
Nicely put. Appreciate it….
October 5th, 2022 at 4:40 pm
Generic for viagra https://search.gmx.com/web/result?q=“My Canadian Pharmacy – Extensive Assortment of Medications – 2022″…
Regards, Fantastic information!…
October 6th, 2022 at 1:47 am
Viagra coupon https://search.seznam.cz/?q=“My Canadian Pharmacy – Extensive Assortment of Medications – 2022″…
Great stuff. Thanks!…
October 6th, 2022 at 5:27 am
Viagra vs viagra https://sanangelolive.com/members/unsafiri...
Seriously a lot of very good data….
October 6th, 2022 at 9:45 am
Viagra alternative …
Well voiced without a doubt! ….
October 6th, 2022 at 3:42 pm
canadian pharmacys https://swisscows.com/en/web?query=“My Canadian Pharmacy – Extensive Assortment of Medications – 2022″…
You actually suggested it well….
October 7th, 2022 at 10:06 am
Viagra great britain …
Awesome postings, Kudos….
October 8th, 2022 at 6:06 am
canadian pharmacies mail order https://search.givewater.com/serp?q=“My Canadian Pharmacy – Extensive Assortment of Medications – 2022″…
You said it wonderfully….
October 8th, 2022 at 11:34 am
canadianpharmacy https://www.bakespace.com/members/profile/Сanadian pharmaceuticals for usa sales/1541108/…
You have made your point quite well…..
October 9th, 2022 at 4:42 am
Canadian viagra …
Whoa tons of superb advice!…
October 9th, 2022 at 9:50 am
Viagra tablets australia https://results.excite.com/serp?q=“My Canadian Pharmacy – Extensive Assortment of Medications – 2022″…
Seriously a lot of terrific tips….
October 9th, 2022 at 2:19 pm
Viagra great britain https://www.infospace.com/serp?q=“My Canadian Pharmacy – Extensive Assortment of Medications – 2022″…
Wow tons of useful info!…
October 10th, 2022 at 6:35 am
Viagra great britain https://headwayapp.co/canadianppharmacy-changelog...
You explained it well!…
October 11th, 2022 at 4:31 am
Viagra tablets https://results.excite.com/serp?q=“My Canadian Pharmacy – Extensive Assortment of Medications – 2022″…
You explained this adequately!…
October 11th, 2022 at 9:53 am
Online viagra https://canadianpharmaceuticalsonline.as.me/schedule.php...
Fantastic content. Thanks a lot!…
October 14th, 2022 at 4:21 am
canadian pharmacies without an rx https://reallygoodemails.com/orderstromectoloverthecounterusa...
Wonderful information, Cheers….