The Comonad.Reader

Is State a Comonad?

Not Costate or rather, Store as we tend to call it today, but actually State s itself?

Let's see!

(more...)

A common occurrence in category theory is the adjoint triple. This is a pair of adjunctions relating three functors:

F ⊣ G ⊣ H
F ⊣ G, G ⊣ H

Perhaps part of the reason they are so common is that (co)limits form one:

colim ⊣ Δ ⊣ lim

where Δ : C -> C^J is the diagonal functor, which takes objects in C to the constant functor returning that object. A version of this shows up in Haskell (with some extensions) and dependent type theories, as:

∃ ⊣ Const ⊣ ∀
Σ ⊣ Const ⊣ Π

where, if we only care about quantifying over a single variable, existential and sigma types can be seen as a left adjoint to a diagonal functor that maps types into constant type families (either over * for the first triple in Haskell, or some other type for the second in a dependently typed language), while universal and pi types can be seen as a right adjoint to the same.

It's not uncommon to see the above information in type theory discussion forums. But, there are a few cute properties and examples of adjoint triples that I haven't really seen come up in such contexts.

To begin, we can compose the two adjunctions involved, since the common functor ensures things match up. By calculating on the hom definition, we can see:

Hom(FGA, B)     Hom(GFA, B)
    ~=              ~=
Hom(GA, GB)     Hom(FA, HB)
    ~=              ~=
Hom(A, HGB)     Hom(A, GHB)

So there are two ways to compose the adjunctions, giving two induced adjunctions:

FG ⊣ HG,  GF ⊣ GH

And there is something special about these adjunctions. Note that FG is the comonad for the F ⊣ G adjunction, while HG is the monad for the G ⊣ H adjunction. Similarly, GF is the F ⊣ G monad, and GH is the G ⊣ H comonad. So each adjoint triple gives rise to two adjunctions between monads and comonads.

The second of these has another interesting property. We often want to consider the algebras of a monad, and coalgebras of a comonad. The (co)algebra operations with carrier A have type:

alg   : GFA -> A
coalg : A -> GHA

but these types are isomorphic according to the GF ⊣ GH adjunction. Thus, one might guess that GF monad algebras are also GH comonad coalgebras, and that in such a situation, we actually have some structure that can be characterized both ways. In fact this is true for any monad left adjoint to a comonad; [0] but all adjoint triples give rise to these.

The first adjunction actually turns out to be more familiar for the triple examples above, though. (Edit: [2]) If we consider the Σ ⊣ Const ⊣ Π adjunction, where:

Σ Π : (A -> Type) -> Type
Const : Type -> (A -> Type)

we get:

ΣConst : Type -> Type
ΣConst B = A × B
ΠConst : Type -> Type
ΠConst B = A -> B

So this is the familiar adjunction:

A × - ⊣ A -> -

But, there happens to be a triple that is a bit more interesting for both cases. It refers back to categories of functors vs. bare type constructors mentioned in previous posts. So, suppose we have a category called Con whose objects are (partially applied) type constructors (f, g) with kind * -> *, and arrows are polymorphic functions with types like:

 
forall x. f x -> g x
 

And let us further imagine that there is a similar category, called Func, except its objects are the things with Functor instances. Now, there is a functor:

U : Func -> Con

that 'forgets' the functor instance requirement. This functor is in the middle of an adjoint triple:

F ⊣ U ⊣ C
F, C : Con -> Func

where F creates the free functor over a type constructor, and C creates the cofree functor over a type constructor. These can be written using the types:

 
data F f a = forall e. F (e -> a) (f e)
newtype C f a = C (forall r. (a -> r) -> f r)
 

and these types will also serve as the types involved in the composite adjunctions:

FU ⊣ CU : Func -> Func
UF ⊣ UC : Con -> Con

Now, CU is a monad on functors, and the Yoneda lemma tells us that it is actually the identity monad. Similarly, FU is a comonad, and the co-Yoneda lemma tells us that it is the identity comonad (which makes sense, because identity is self-adjoint; and the above is why F and C are often named (Co)Yoneda in Haskell examples).

On the other hand, UF is a monad on type constructors (note, U isn't represented in the Haskell types; F and C just play triple duty, and the constraints on f control what's going on):

 
eta :: f a -> F f a
eta = F id
 
transform :: (forall x. f x -> g x) -> F f a -> F g a
transform tr (F g x) = F g (tr x)
 
mu :: F (F f) a -> F f a
mu (F g (F h x)) = F (g . h) x
 

and UC is a comonad:

 
epsilon :: C f a -> f a
epsilon (C e) = e id
 
transform' :: (forall x. f x -> g x) -> C f a -> C g a
transform' tr (C e) = C (tr . e)
 
delta :: C f a -> C (C f) a
delta (C e) = C $ \h -> C $ \g -> e (g . h)
 

These are not the identity (co)monad, but this is the case where we have algebras and coalgebras that are equivalent. So, what are the (co)algebras? If we consider UF (and unpack the definitions somewhat):

 
alg :: forall e. (e -> a, f e) -> f a
alg (id, x) = x
alg (g . h, x) = alg (g, alg (h, x))
 

and for UC:

 
coalg :: f a -> forall r. (a -> r) -> f r
coalg x id = x
coalg x (g . h) = coalg (coalg x h) g
 

in other words, (co)algebra actions of these (co)monads are (mangled) fmap implementations, and the commutativity requirements are exactly what is required to be a law abiding instance. So the (co)algebras are exactly the Functors. [1]

There are, of course, many other examples of adjoint triples. And further, there are even adjoint quadruples, which in turn give rise to adjoint triples of (co)monads. Hopefully this has sparked some folks' interest in finding and studying more interesting examples.

[0]: Another exmaple is A × - ⊣ A -> - where the A in question is a monoid. (Co)monad (co)algebras of these correspond to actions of the monoid on the carrier set.

[1]: This shouldn't be too surprising, because having a category of (co)algebraic structures that is equivalent to the category of (co)algebras of the (co)monad that comes from the (co)free-forgetful adjunction is the basis for doing algebra in category theory (with (co)monads, at least). However, it is somewhat unusual for a forgetful functor to have both a left and right adjoint. In many cases, something is either algebraic or coalgebraic, and not both.

[2]: Urs Schreiber informed me of an interesting interpretation of the ConstΣ ⊣ ConstΠ adjunction. If you are familiar with modal logic and the possible worlds semantics thereof, you can probably imagine that we could model it using something like P : W -> Type, where W is the type of possible worlds, and propositions are types. Then values of type Σ P demonstrate that P holds in particular worlds, while values of type Π P demonstrate that it holds in all worlds. Const turns these types back into world-indexed 'propositions,' so ConstΣ is the possibility modality and ConstΠ is the necessity modality.

In the last couple posts I've used some 'free' constructions, and not remarked too much on how they arise. In this post, I'd like to explore them more. This is going to be something of a departure from the previous posts, though, since I'm not going to worry about thinking precisely about bottom/domains. This is more an exercise in applying some category theory to Haskell, "fast and loose".

(Advance note: for some continuous code to look at see this file.)

First, it'll help to talk about how some categories can work in Haskell. For any kind k made of * and (->), [0] we can define a category of type constructors. Objects of the category will be first-class [1] types of that kind, and arrows will be defined by the following type family:

 
newtype Transformer f g = Transform { ($$) :: forall i. f i ~> g i }
 
type family (~>) :: k -> k -> * where
  (~>) = (->)
  (~>) = Transformer
 
type a < -> b = (a -> b, b -> a)
type a < ~> b = (a ~> b, b ~> a)
 

So, for a base case, * has monomorphic functions as arrows, and categories for higher kinds have polymorphic functions that saturate the constructor:

 
  Int ~> Char = Int -> Char
  Maybe ~> [] = forall a. Maybe a -> [a]
  Either ~> (,) = forall a b. Either a b -> (a, b)
  StateT ~> ReaderT = forall s m a. StateT s m a -> ReaderT s m a
 

We can of course define identity and composition for these, and it will be handy to do so:

 
class Morph (p :: k -> k -> *) where
  id :: p a a
  (.) :: p b c -> p a b -> p a c
 
instance Morph (->) where
  id x = x
  (g . f) x = g (f x)
 
instance Morph ((~>) :: k -> k -> *)
      => Morph (Transformer :: (i -> k) -> (i -> k) -> *) where
  id = Transform id
  Transform f . Transform g = Transform $ f . g
 

These categories can be looked upon as the most basic substrates in Haskell. For instance, every type of kind * -> * is an object of the relevant category, even if it's a GADT or has other structure that prevents it from being nicely functorial.

The category for * is of course just the normal category of types and functions we usually call Hask, and it is fairly analogous to the category of sets. One common activity in category theory is to study categories of sets equipped with extra structure, and it turns out we can do this in Haskell, as well. And it even makes some sense to study categories of structures over any of these type categories.

When we equip our types with structure, we often use type classes, so that's how I'll do things here. Classes have a special status socially in that we expect people to only define instances that adhere to certain equational rules. This will take the place of equations that we are not able to state in the Haskell type system, because it doesn't have dependent types. So using classes will allow us to define more structures that we normally would, if only by convention.

So, if we have a kind k, then a corresponding structure will be σ :: k -> Constraint. We can then define the category (k,σ) as having objects t :: k such that there is an instance σ t. Arrows are then taken to be f :: t ~> u such that f "respects" the operations of σ.

As a simple example, we have:

 
  k = *
  σ = Monoid :: * -> Constraint
 
  Sum Integer, Product Integer, [Integer] :: (*, Monoid)
 
  f :: (Monoid m, Monoid n) => m -> n
    if f mempty = mempty
       f (m <> n) = f m <> f n
 

This is just the category of monoids in Haskell.

As a side note, we will sometimes be wanting to quantify over these "categories of structures". There isn't really a good way to package together a kind and a structure such that they work as a unit, but we can just add a constraint to the quantification. So, to quantify over all Monoids, we'll use 'forall m. Monoid m => ...'.

Now, once we have these categories of structures, there is an obvious forgetful functor back into the unadorned category. We can then look for free and cofree functors as adjoints to this. More symbolically:

 
  Forget σ :: (k,σ) -> k
  Free   σ :: k -> (k,σ)
  Cofree σ :: k -> (k,σ)
 
  Free σ ⊣ Forget σ ⊣ Cofree σ
 

However, what would be nicer (for some purposes) than having to look for these is being able to construct them all systematically, without having to think much about the structure σ.

Category theory gives a hint at this, too, in the form of Kan extensions. In category terms they look like:

  p : C -> C'
  f : C -> D
  Ran p f : C' -> D
  Lan p f : C' -> D

  Ran p f c' = end (c : C). Hom_C'(c', p c) ⇒ f c
  Lan p f c' = coend (c : c). Hom_C'(p c, c') ⊗ f c

where ⇒ is a "power" and ⊗ is a copower, which are like being able to take exponentials and products by sets (or whatever the objects of the hom category are), instead of other objects within the category. Ends and coends are like universal and existential quantifiers (as are limits and colimits, but ends and coends involve mixed-variance).

Some handy theorems relate Kan extensions and adjoint functors:

  if L ⊣ R
  then L = Ran R Id and R = Lan L Id

  if Ran R Id exists and is absolute
  then Ran R Id ⊣ R

  if Lan L Id exists and is absolute
  then L ⊣ Lan L Id

  Kan P F is absolute iff forall G. (G . Kan P F) ~= Kan P (G . F)

It turns out we can write down Kan extensions fairly generally in Haskell. Our restricted case is:

 
  p = Forget σ :: (k,σ) -> k
  f = Id :: (k,σ) -> (k,σ)
 
  Free   σ = Ran (Forget σ) Id :: k -> (k,σ)
  Cofree σ = Lan (Forget σ) Id :: k -> (k,σ)
 
  g :: (k,σ) -> j
  g . Free   σ = Ran (Forget σ) g
  g . Cofree σ = Lan (Forget σ) g
 

As long as the final category is like one of our type constructor categories, ends are universal quantifiers, powers are function types, coends are existential quantifiers and copowers are product spaces. This only breaks down for our purposes when g is contravariant, in which case they are flipped. For higher kinds, these constructions occur point-wise. So, we can break things down into four general cases, each with cases for each arity:

 
newtype Ran0 σ p (f :: k -> *) a =
  Ran0 { ran0 :: forall r. σ r => (a ~> p r) -> f r }
 
newtype Ran1 σ p (f :: k -> j -> *) a b =
  Ran1 { ran1 :: forall r. σ r => (a ~> p r) -> f r b }
 
-- ...
 
data RanOp0 σ p (f :: k -> *) a =
  forall e. σ e => RanOp0 (a ~> p e) (f e)
 
-- ...
 
data Lan0 σ p (f :: k -> *) a =
  forall e. σ e => Lan0 (p e ~> a) (f e)
 
data Lan1 σ p (f :: k -> j -> *) a b =
  forall e. σ e => Lan1 (p e ~> a) (f e b)
 
-- ...
 
data LanOp0 σ p (f :: k -> *) a =
  LanOp0 { lan0 :: forall r. σ r => (p r -> a) -> f r }
 
-- ...
 

The more specific proposed (co)free definitions are:

 
type family Free   :: (k -> Constraint) -> k -> k
type family Cofree :: (k -> Constraint) -> k -> k
 
newtype Free0 σ a = Free0 { gratis0 :: forall r. σ r => (a ~> r) -> r }
type instance Free = Free0
 
newtype Free1 σ f a = Free1 { gratis1 :: forall g. σ g => (f ~> g) -> g a }
type instance Free = Free1
 
-- ...
 
data Cofree0 σ a = forall e. σ e => Cofree0 (e ~> a) e
type instance Cofree = Cofree0
 
data Cofree1 σ f a = forall g. σ g => Cofree1 (g ~> f) (g a)
type instance Cofree = Cofree1
 
-- ...
 

We can define some handly classes and instances for working with these types, several of which generalize existing Haskell concepts:

 
class Covariant (f :: i -> j) where
  comap :: (a ~> b) -> (f a ~> f b)
 
class Contravariant f where
  contramap :: (b ~> a) -> (f a ~> f b)
 
class Covariant m => Monad (m :: i -> i) where
  pure :: a ~> m a
  join :: m (m a) ~> m a
 
class Covariant w => Comonad (w :: i -> i) where
  extract :: w a ~> a
  split :: w a ~> w (w a)
 
class Couniversal σ f | f -> σ where
  couniversal :: σ r => (a ~> r) -> (f a ~> r)
 
class Universal σ f | f -> σ where
  universal :: σ e => (e ~> a) -> (e ~> f a)
 
instance Covariant (Free0 σ) where
  comap f (Free0 e) = Free0 (e . (.f))
 
instance Monad (Free0 σ) where
  pure x = Free0 $ \k -> k x
  join (Free0 e) = Free0 $ \k -> e $ \(Free0 e) -> e k
 
instance Couniversal σ (Free0 σ) where
  couniversal h (Free0 e) = e h
 
-- ...
 

The only unfamiliar classes here should be (Co)Universal. They are for witnessing the adjunctions that make Free σ the initial σ and Cofree σ the final σ in the relevant way. Only one direction is given, since the opposite is very easy to construct with the (co)monad structure.

Free σ is a monad and couniversal, Cofree σ is a comonad and universal.

We can now try to convince ourselves that Free σ and Cofree σ are absolute Here are some examples:

 
free0Absolute0 :: forall g σ a. (Covariant g, σ (Free σ a))
               => g (Free0 σ a) < -> Ran σ Forget g a
free0Absolute0 = (l, r)
 where
 l :: g (Free σ a) -> Ran σ Forget g a
 l g = Ran0 $ \k -> comap (couniversal $ remember0 . k) g
 
 r :: Ran σ Forget g a -> g (Free σ a)
 r (Ran0 e) = e $ Forget0 . pure
 
free0Absolute1 :: forall (g :: * -> * -> *) σ a x. (Covariant g, σ (Free σ a))
               => g (Free0 σ a) x < -> Ran σ Forget g a x
free0Absolute1 = (l, r)
 where
 l :: g (Free σ a) x -> Ran σ Forget g a x
 l g = Ran1 $ \k -> comap (couniversal $ remember0 . k) $$ g
 
 r :: Ran σ Forget g a x -> g (Free σ a) x
 r (Ran1 e) = e $ Forget0 . pure
 
free0Absolute0Op :: forall g σ a. (Contravariant g, σ (Free σ a))
                 => g (Free0 σ a) < -> RanOp σ Forget g a
free0Absolute0Op = (l, r)
 where
 l :: g (Free σ a) -> RanOp σ Forget g a
 l = RanOp0 $ Forget0 . pure
 
 r :: RanOp σ Forget g a -> g (Free σ a)
 r (RanOp0 h g) = contramap (couniversal $ remember0 . h) g
 
-- ...
 

As can be seen, the definitions share a lot of structure. I'm quite confident that with the right building blocks these could be defined once for each of the four types of Kan extensions, with types like:

 
freeAbsolute
  :: forall g σ a. (Covariant g, σ (Free σ a))
  => g (Free σ a) < ~> Ran σ Forget g a
 
cofreeAbsolute
  :: forall g σ a. (Covariant g, σ (Cofree σ a))
  => g (Cofree σ a) < ~> Lan σ Forget g a
 
freeAbsoluteOp
  :: forall g σ a. (Contravariant g, σ (Free σ a))
  => g (Free σ a) < ~> RanOp σ Forget g a
 
cofreeAbsoluteOp
  :: forall g σ a. (Contravariant g, σ (Cofree σ a))
  => g (Cofree σ a) < ~> LanOp σ Forget g a
 

However, it seems quite difficult to structure things in a way such that GHC will accept the definitions. I've successfully written freeAbsolute using some axioms, but turning those axioms into class definitions and the like seems impossible.

Anyhow, the punchline is that we can prove absoluteness using only the premise that there is a valid σ instance for Free σ and Cofree σ. This tends to be quite easy; we just borrow the structure of the type we are quantifying over. This means that in all these cases, we are justified in saying that Free σ ⊣ Forget σ ⊣ Cofree σ, and we have a very generic presentations of (co)free structures in Haskell. So let's look at some.

We've already seen Free Monoid, and last time we talked about Free Applicative, and its relation to traversals. But, Applicative is to traversal as Functor is to lens, so it may be interesting to consider constructions on that. Both Free Functor and Cofree Functor make Functors:

 
instance Functor (Free1 Functor f) where
  fmap f (Free1 e) = Free1 $ fmap f . e
 
instance Functor (Cofree1 Functor f) where
  fmap f (Cofree1 h e) = Cofree1 h (fmap f e)
 

And of course, they are (co)monads, covariant functors and (co)universal among Functors. But, it happens that I know some other types with these properties:

 
data CoYo f a = forall e. CoYo (e -> a) (f e)
 
instance Covariant CoYo where
  comap f = Transform $ \(CoYo h e) -> CoYo h (f $$ e)
 
instance Monad CoYo where
  pure = Transform $ CoYo id
  join = Transform $ \(CoYo h (CoYo h' e)) -> CoYo (h . h') e
 
instance Functor (CoYo f) where
  fmap f (CoYo h e) = CoYo (f . h) e
 
instance Couniversal Functor CoYo where
  couniversal tr = Transform $ \(CoYo h e) -> fmap h (tr $$ e)
 
newtype Yo f a = Yo { oy :: forall r. (a -> r) -> f r }
 
instance Covariant Yo where
  comap f = Transform $ \(Yo e) -> Yo $ (f $$) . e
 
instance Comonad Yo where
  extract = Transform $ \(Yo e) -> e id
  split = Transform $ \(Yo e) -> Yo $ \k -> Yo $ \k' -> e $ k' . k
 
instance Functor (Yo f) where
  fmap f (Yo e) = Yo $ \k -> e (k . f)
 
instance Universal Functor Yo where
  universal tr = Transform $ \e -> Yo $ \k -> tr $$ fmap k e
 

These are the types involved in the (co-)Yoneda lemma. CoYo is a monad, couniversal among functors, and CoYo f is a Functor. Yo is a comonad, universal among functors, and is always a Functor. So, are these equivalent types?

 
coyoIso :: CoYo < ~> Free Functor
coyoIso = (Transform $ couniversal pure, Transform $ couniversal pure)
 
yoIso :: Yo < ~> Cofree Functor
yoIso = (Transform $ universal extract, Transform $ universal extract)
 

Indeed they are. And similar identities hold for the contravariant versions of these constructions.

I don't have much of a use for this last example. I suppose to be perfectly precise, I should point out that these uses of (Co)Yo are not actually part of the (co-)Yoneda lemma. They are two different constructions. The (co-)Yoneda lemma can be given in terms of Kan extensions as:

 
yoneda :: Ran Id f < ~> f
 
coyoneda :: Lan Id f < ~> f
 

But, the use of (Co)Yo to make Functors out of things that aren't necessarily is properly thought of in other terms. In short, we have some kind of category of Haskell types with only identity arrows---it is discrete. Then any type constructor, even non-functorial ones, is certainly a functor from said category (call it Haskrete) into the normal one (Hask). And there is an inclusion functor from Haskrete into Hask:

             F
 Haskrete -----> Hask
      |        /|
      |       /
      |      /
Incl  |     /
      |    /  Ran/Lan Incl F
      |   /
      |  /
      v /
    Hask

So, (Co)Free Functor can also be thought of in terms of these Kan extensions involving the discrete category.

To see more fleshed out, loadable versions of the code in this post, see this file. I may also try a similar Agda development at a later date, as it may admit the more general absoluteness constructions easier.

[0]: The reason for restricting ourselves to kinds involving only * and (->) is that they work much more simply than data kinds. Haskell values can't depend on type-level entities without using type classes. For *, this is natural, but for something like Bool -> *, it is more natural for transformations to be able to inspect the booleans, and so should be something more like forall b. InspectBool b => f b -> g b.

[1]: First-class types are what you get by removing type families and synonyms from consideration. The reason for doing so is that these can't be used properly as parameters and the like, except in cases where they reduce to some other type that is first-class. For example, if we define:

 
type I a = a
 

even though GHC will report I :: * -> *, it is not legal to write Transform I I.

Last time I looked at free monoids, and noticed that in Haskell lists don't really cut it. This is a consequence of laziness and general recursion. To model a language with those properties, one needs to use domains and monotone, continuous maps, rather than sets and total functions (a call-by-value language with general recursion would use domains and strict maps instead).

This time I'd like to talk about some other examples of this, and point out how doing so can (perhaps) resolve some disagreements that people have about the specific cases.

The first example is not one that I came up with: induction. It's sometimes said that Haskell does not have inductive types at all, or that we cannot reason about functions on its data types by induction. However, I think this is (techincally) inaccurate. What's true is that we cannot simply pretend that that our types are sets and use the induction principles for sets to reason about Haskell programs. Instead, one has to figure out what inductive domains would be, and what their proof principles are.

Fortunately, there are some papers about doing this. The most recent (that I'm aware of) is Generic Fibrational Induction. I won't get too into the details, but it shows how one can talk about induction in a general setting, where one has a category that roughly corresponds to the type theory/programming language, and a second category of proofs that is 'indexed' by the first category's objects. Importantly, it is not required that the second category is somehow 'part of' the type theory being reasoned about, as is often the case with dependent types, although that is also a special case of their construction.

One of the results of the paper is that this framework can be used to talk about induction principles for types that don't make sense as sets. Specifically:

 
newtype Hyp = Hyp ((Hyp -> Int) -> Int)
 

the type of "hyperfunctions". Instead of interpreting this type as a set, where it would effectively require a set that is isomorphic to the power set of its power set, they interpret it in the category of domains and strict functions mentioned earlier. They then construct the proof category in a similar way as one would for sets, except instead of talking about predicates as subsets, we talk about sub-domains instead. Once this is done, their framework gives a notion of induction for this type.

This example is suitable for ML (and suchlike), due to the strict functions, and sort of breaks the idea that we can really get away with only thinking about sets, even there. Sets are good enough for some simple examples (like flat domains where we don't care about ⊥), but in general we have to generalize induction itself to apply to all types in the 'good' language.

While I haven't worked out how the generic induction would work out for Haskell, I have little doubt that it would, because ML actually contains all of Haskell's data types (and vice versa). So the fact that the framework gives meaning to induction for ML implies that it does so for Haskell. If one wants to know what induction for Haskell's 'lazy naturals' looks like, they can study the ML analogue of:

 
data LNat = Zero | Succ (() -> LNat)
 

because function spaces lift their codomain, and make things 'lazy'.

----

The other example I'd like to talk about hearkens back to the previous article. I explained how foldMap is the proper fundamental method of the Foldable class, because it can be massaged to look like:

 
foldMap :: Foldable f => f a -> FreeMonoid a
 

and lists are not the free monoid, because they do not work properly for various infinite cases.

I also mentioned that foldMap looks a lot like traverse:

 
foldMap  :: (Foldable t   , Monoid m)      => (a -> m)   -> t a -> m
traverse :: (Traversable t, Applicative f) => (a -> f b) -> t a -> f (t b)
 

And of course, we have Monoid m => Applicative (Const m), and the functions are expected to agree in this way when applicable.

Now, people like to get in arguments about whether traversals are allowed to be infinite. I know Ed Kmett likes to argue that they can be, because he has lots of examples. But, not everyone agrees, and especially people who have papers proving things about traversals tend to side with the finite-only side. I've heard this includes one of the inventors of Traversable, Conor McBride.

In my opinion, the above disagreement is just another example of a situation where we have a generic notion instantiated in two different ways, and intuition about one does not quite transfer to the other. If you are working in a language like Agda or Coq (for proving), you will be thinking about traversals in the context of sets and total functions. And there, traversals are finite. But in Haskell, there are infinitary cases to consider, and they should work out all right when thinking about domains instead of sets. But I should probably put forward some argument for this position (and even if I don't need to, it leads somewhere else interesting).

One example that people like to give about finitary traversals is that they can be done via lists. Given a finite traversal, we can traverse to get the elements (using Const [a]), traverse the list, then put them back where we got them by traversing again (using State [a]). Usually when you see this, though, there's some subtle cheating in relying on the list to be exactly the right length for the second traversal. It will be, because we got it from a traversal of the same structure, but I would expect that proving the function is actually total to be a lot of work. Thus, I'll use this as an excuse to do my own cheating later.

Now, the above uses lists, but why are we using lists when we're in Haskell? We know they're deficient in certain ways. It turns out that we can give a lot of the same relevant structure to the better free monoid type:

 
newtype FM a = FM (forall m. Monoid m => (a -> m) -> m) deriving (Functor)
 
instance Applicative FM where
  pure x = FM ($ x)
  FM ef < *> FM ex = FM $ \k -> ef $ \f -> ex $ \x -> k (f x)
 
instance Monoid (FM a) where
  mempty = FM $ \_ -> mempty
  mappend (FM l) (FM r) = FM $ \k -> l k <> r k
 
instance Foldable FM where
  foldMap f (FM e) = e f
 
newtype Ap f b = Ap { unAp :: f b }
 
instance (Applicative f, Monoid b) => Monoid (Ap f b) where
  mempty = Ap $ pure mempty
  mappend (Ap l) (Ap r) = Ap $ (<>) < $> l < *> r
 
instance Traversable FM where
  traverse f (FM e) = unAp . e $ Ap . fmap pure . f
 

So, free monoids are Monoids (of course), Foldable, and even Traversable. At least, we can define something with the right type that wouldn't bother anyone if it were written in a total language with the right features, but in Haskell it happens to allow various infinite things that people don't like.

Now it's time to cheat. First, let's define a function that can take any Traversable to our free monoid:

 
toFreeMonoid :: Traversable t => t a -> FM a
toFreeMonoid f = FM $ \k -> getConst $ traverse (Const . k) f
 

Now let's define a Monoid that's not a monoid:

 
data Cheat a = Empty | Single a | Append (Cheat a) (Cheat a)
 
instance Monoid (Cheat a) where
  mempty = Empty
  mappend = Append
 

You may recognize this as the data version of the free monoid from the previous article, where we get the real free monoid by taking a quotient. using this, we can define an Applicative that's not valid:

 
newtype Cheating b a =
  Cheating { prosper :: Cheat b -> a } deriving (Functor)
 
instance Applicative (Cheating b) where
  pure x = Cheating $ \_ -> x
 
  Cheating f < *> Cheating x = Cheating $ \c -> case c of
    Append l r -> f l (x r)
 

Given these building blocks, we can define a function to relabel a traversable using a free monoid:

 
relabel :: Traversable t => t a -> FM b -> t b
relabel t (FM m) = propser (traverse (const hope) t) (m Single)
 where
 hope = Cheating $ \c -> case c of
   Single x -> x
 

And we can implement any traversal by taking a trip through the free monoid:

 
slowTraverse
  :: (Applicative f, Traversable t) => (a -> f b) -> t a -> f (t b)
slowTraverse f t = fmap (relabel t) . traverse f . toFreeMonoid $ t
 

And since we got our free monoid via traversing, all the partiality I hid in the above won't blow up in practice, rather like the case with lists and finite traversals.

Arguably, this is worse cheating. It relies on the exact association structure to work out, rather than just number of elements. The reason is that for infinitary cases, you cannot flatten things out, and there's really no way to detect when you have something infinitary. The finitary traversals have the luxury of being able to reassociate everything to a canonical form, while the infinite cases force us to not do any reassociating at all. So this might be somewhat unsatisfying.

But, what if we didn't have to cheat at all? We can get the free monoid by tweaking foldMap, and it looks like traverse, so what happens if we do the same manipulation to the latter?

It turns out that lens has a type for this purpose, a slight specialization of which is:

 
newtype Bazaar a b t =
  Bazaar { runBazaar :: forall f. Applicative f => (a -> f b) -> f t }
 

Using this type, we can reorder traverse to get:

 
howBizarre :: Traversable t => t a -> Bazaar a b (t b)
howBizarre t = Bazaar $ \k -> traverse k t
 

But now, what do we do with this? And what even is it? [1]

If we continue drawing on intuition from Foldable, we know that foldMap is related to the free monoid. Traversable has more indexing, and instead of Monoid uses Applicative. But the latter are actually related to the former; Applicatives are monoidal (closed) functors. And it turns out, Bazaar has to do with free Applicatives.

If we want to construct free Applicatives, we can use our universal property encoding trick:

 
newtype Free p f a =
  Free { gratis :: forall g. p g => (forall x. f x -> g x) -> g a }
 

This is a higher-order version of the free p, where we parameterize over the constraint we want to use to represent structures. So Free Applicative f is the free Applicative over a type constructor f. I'll leave the instances as an exercise.

Since free monoid is a monad, we'd expect Free p to be a monad, too. In this case, it is a McBride style indexed monad, as seen in The Kleisli Arrows of Outrageous Fortune.

 
type f ~> g = forall x. f x -> g x
 
embed :: f ~> Free p f
embed fx = Free $ \k -> k fx
 
translate :: (f ~> g) -> Free p f ~> Free p g
translate tr (Free e) = Free $ \k -> e (k . tr)
 
collapse :: Free p (Free p f) ~> Free p f
collapse (Free e) = Free $ \k -> e $ \(Free e') -> e' k
 

That paper explains how these are related to Atkey style indexed monads:

 
data At key i j where
  At :: key -> At key i i
 
type Atkey m i j a = m (At a j) i
 
ireturn :: IMonad m => a -> Atkey m i i a
ireturn = ...
 
ibind :: IMonad m => Atkey m i j a -> (a -> Atkey m j k b) -> Atkey m i k b
ibind = ...
 

It turns out, Bazaar is exactly the Atkey indexed monad derived from the Free Applicative indexed monad (with some arguments shuffled) [2]:

 
hence :: Bazaar a b t -> Atkey (Free Applicative) t b a
hence bz = Free $ \tr -> runBazaar bz $ tr . At
 
forth :: Atkey (Free Applicative) t b a -> Bazaar a b t
forth fa = Bazaar $ \g -> gratis fa $ \(At a) -> g a
 
imap :: (a -> b) -> Bazaar a i j -> Bazaar b i j
imap f (Bazaar e) = Bazaar $ \k -> e (k . f)
 
ipure :: a -> Bazaar a i i
ipure x = Bazaar ($ x)
 
(>>>=) :: Bazaar a j i -> (a -> Bazaar b k j) -> Bazaar b k i
Bazaar e >>>= f = Bazaar $ \k -> e $ \x -> runBazaar (f x) k
 
(>==>) :: (s -> Bazaar i o t) -> (i -> Bazaar a b o) -> s -> Bazaar a b t
(f >==> g) x = f x >>>= g
 

As an aside, Bazaar is also an (Atkey) indexed comonad, and the one that characterizes traversals, similar to how indexed store characterizes lenses. A Lens s t a b is equivalent to a coalgebra s -> Store a b t. A traversal is a similar Bazaar coalgebra:

 
  s -> Bazaar a b t
    ~
  s -> forall f. Applicative f => (a -> f b) -> f t
    ~
  forall f. Applicative f => (a -> f b) -> s -> f t
 

It so happens that Kleisli composition of the Atkey indexed monad above (>==>) is traversal composition.

Anyhow, Bazaar also inherits Applicative structure from Free Applicative:

 
instance Functor (Bazaar a b) where
  fmap f (Bazaar e) = Bazaar $ \k -> fmap f (e k)
 
instance Applicative (Bazaar a b) where
  pure x = Bazaar $ \_ -> pure x
  Bazaar ef < *> Bazaar ex = Bazaar $ \k -> ef k < *> ex k
 

This is actually analogous to the Monoid instance for the free monoid; we just delegate to the underlying structure.

The more exciting thing is that we can fold and traverse over the first argument of Bazaar, just like we can with the free monoid:

 
bfoldMap :: Monoid m => (a -> m) -> Bazaar a b t -> m
bfoldMap f (Bazaar e) = getConst $ e (Const . f)
 
newtype Comp g f a = Comp { getComp :: g (f a) } deriving (Functor)
 
instance (Applicative f, Applicative g) => Applicative (Comp g f) where
  pure = Comp . pure . pure
  Comp f < *> Comp x = Comp $ liftA2 (< *>) f x
 
btraverse
  :: (Applicative f) => (a -> f a') -> Bazaar a b t -> Bazaar a' b t
btraverse f (Bazaar e) = getComp $ e (c . fmap ipure . f)
 

This is again analogous to the free monoid code. Comp is the analogue of Ap, and we use ipure in traverse. I mentioned that Bazaar is a comonad:

 
extract :: Bazaar b b t -> t
extract (Bazaar e) = runIdentity $ e Identity
 

And now we are finally prepared to not cheat:

 
honestTraverse
  :: (Applicative f, Traversable t) => (a -> f b) -> t a -> f (t b)
honestTraverse f = fmap extract . btraverse f . howBizarre
 

So, we can traverse by first turning out Traversable into some structure that's kind of like the free monoid, except having to do with Applicative, traverse that, and then pull a result back out. Bazaar retains the information that we're eventually building back the same type of structure, so we don't need any cheating.

To pull this back around to domains, there's nothing about this code to object to if done in a total language. But, if we think about our free Applicative-ish structure, in Haskell, it will naturally allow infinitary expressions composed of the Applicative operations, just like the free monoid will allow infinitary monoid expressions. And this is okay, because some Applicatives can make sense of those, so throwing them away would make the type not free, in the same way that even finite lists are not the free monoid in Haskell. And this, I think, is compelling enough to say that infinite traversals are right for Haskell, just as they are wrong for Agda.

For those who wish to see executable code for all this, I've put a files here and here. The latter also contains some extra goodies at the end that I may talk about in further installments.

[1] Truth be told, I'm not exactly sure.

[2] It turns out, you can generalize Bazaar to have a correspondence for every choice of p

 
newtype Bizarre p a b t =
  Bizarre { bizarre :: forall f. p f => (a -> f b) -> f t }
 

hence and forth above go through with the more general types. This can be seen here.

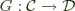Recently, a fellow in category land discovered a fact that we in Haskell land have actually known for a while (in addition to things most of us probably don't). Specifically, given two categories and , a functor , and provided some conditions in hold, there exists a monad , the codensity monad of .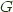

In category theory, the codensity monad is given by the rather frightening expression:

(more...)

Andrej Bauer recently gave a really nice talk on how you can exploit side-effects to make a faster version of Martin Escardo's pseudo-paradoxical combinators.

A video of his talk is available over on his blog, and his presentation is remarkably clear, and would serve as a good preamble to the code I'm going to present below.

Andrej gave a related invited talk back at MSFP 2008 in Iceland, and afterwards over lunch I cornered him (with Dan Piponi) and explained how you could use parametricity to close over the side-effects of monads (or arrows, etc) but I think that trick was lost in the chaos of the weekend, so I've chosen to resurrect it here, and improve it to handle some of his more recent performance enhancements, and show that you don't need side-effects to speed up the search after all!

(more...)

Last time we derived an entailment relation for constraints, now let's get some use out of it.

Reflecting Classes and Instances

Most of the implications we use on a day to day basis come from our class and instance declarations, but last time we only really dealt with constraint products.

(more...)

Max Bolingbroke has done a wonderful job on adding Constraint kinds to GHC.

Constraint Kinds adds a new kind Constraint, such that Eq :: * -> Constraint, Monad :: (* -> *) -> Constraint, but since it is a kind, we can make type families for constraints, and even parameterize constraints on constraints.

So, let's play with them and see what we can come up with!

(more...)

Last time, I showed that we can build a small parsec clone with packrat support.

This time I intend to implement packrat directly on top of Parsec 3.

One of the main topics of discussion when it comes to packrat parsing since Bryan Ford's initial release of Pappy has been the fact that in general you shouldn't use packrat to memoize every rule, and that instead you should apply Amdahl's law to look for the cases where the lookup time is paid back in terms of repetitive evaluation, computation time and the hit rate. This is great news for us, since, we only want to memoize a handful of expensive combinators.

(more...)

You never heard of the Millenium Falcon? It's the ship that made the Kessel Run in 12 parsecs.

I've been working on a parser combinator library called trifecta, and so I decided I'd share some thoughts on parsing.

Packrat parsing (as provided by frisby, pappy, rats! and the Scala parsing combinators) and more traditional recursive descent parsers (like Parsec) are often held up as somehow different.

Today I'll show that you can add monadic parsing to a packrat parser, sacrificing asymptotic guarantees in exchange for the convenient context sensitivity, and conversely how you can easily add packrat parsing to a traditional monadic parser combinator library.

(more...)

Today I hope to start a new series of posts exploring constructive abstract algebra in Haskell.

In particular, I want to talk about a novel encoding of linear functionals, polynomials and linear maps in Haskell, but first we're going to have to build up some common terminology.

Having obtained the blessing of Wolfgang Jeltsch, I replaced the algebra package on hackage with something... bigger, although still very much a work in progress.

(more...)

In the last few posts, I've been talking about how we can derive monads and monad transformers from comonads. Along the way we learned that there are more monads than comonads in Haskell.

The question I hope to answer this time, is whether or not we turn any Haskell Comonad into a comonad transformer.

(more...)

Last time in Monad Transformers from Comonads I showed that given any comonad we can derive the monad-transformer

 
newtype CoT w m a = CoT { runCoT :: w (a -> m r) -> m r
 

and so demonstrated that there are fewer comonads than monads in Haskell, because while every Comonad gives rise to a Monad transformer, there are Monads that do not like IO, ST s, and STM.

I want to elaborate a bit more on this topic.

(more...)

Last time, I showed that we can transform any Comonad in Haskell into a Monad in Haskell.

Today, I'll show that we can go one step further and derive a monad transformer from any comonad!

(more...)

Today I'll show that you can derive a Monad from any old Comonad you have lying around.

(more...)

Last time, I said that I was going to put our cheap new free monad to work, so let's give it a shot.

(more...)

Last time, I started exploring whether or not Codensity was necessary to improve the asymptotic performance of free monads.

This time I'll show that the answer is no; we can get by with something smaller.

(more...)

A couple of years back Janis Voigtländer wrote a nice paper on how one can use the codensity monad to improve the asymptotic complexity of algorithms using the free monads. He didn't use the name Codensity in the paper, but this is essentially the meaning of his type C.

I just returned from running a workshop on domain-specific languages at McMaster University with the more than able assistance of Wren Ng Thornton. Among the many topics covered, I spent a lot of time talking about how to use free monads to build up term languages for various DSLs with simple evaluators, and then made them efficient by using Codensity.

This has been shown to be a sufficient tool for this task, but is it necessary?

(more...)

I have updated the reflection package on hackage to use an idea for avoiding dummy arguments posted to the Haskell cafe mailing list by Bertram Felgenhauer, which adapts nicely to the case of handling Reflection. The reflection package implements the ideas from the Functional Pearl: Implicit Configurations paper by Oleg Kiselyov and Chung-chieh Shan.

Now, you no longer need to use big scary undefineds throughout your code and can instead program with implicit configurations more naturally, using Applicative and Monad sugar.

(more...)

I want to spend some more time talking about Kan extensions, composition of Kan extensions, and the relationship between a monad and the monad generated by a monad.

But first, I want to take a moment to recall adjunctions and show how they relate to some standard (co)monads, before tying them back to Kan extensions.

Adjunctions 101

An adjunction between categories and consists of a pair of functors 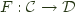, and 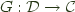and a natural isomorphism:

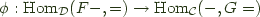
We call 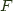the left adjoint functor, and 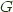the right adjoint functor and 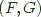an adjoint pair, and write this relationship as

(more...)