Mon 25 May 2015
Categories of Structures in Haskell
Posted by Dan Doel under Category Theory , Comonads , Data Structures , Haskell , Kan Extensions , Mathematics , Monads , Type Hackery , Uncategorized[510] Comments
In the last couple posts I've used some 'free' constructions, and not remarked too much on how they arise. In this post, I'd like to explore them more. This is going to be something of a departure from the previous posts, though, since I'm not going to worry about thinking precisely about bottom/domains. This is more an exercise in applying some category theory to Haskell, "fast and loose".
(Advance note: for some continuous code to look at see this file.)
First, it'll help to talk about how some categories can work in Haskell. For any kind k made of * and (->), [0] we can define a category of type constructors. Objects of the category will be first-class [1] types of that kind, and arrows will be defined by the following type family:
newtype Transformer f g = Transform { ($$) :: forall i. f i ~> g i } type family (~>) :: k -> k -> * where (~>) = (->) (~>) = Transformer type a < -> b = (a -> b, b -> a) type a < ~> b = (a ~> b, b ~> a)
So, for a base case, * has monomorphic functions as arrows, and categories for higher kinds have polymorphic functions that saturate the constructor:
Int ~> Char = Int -> Char Maybe ~> [] = forall a. Maybe a -> [a] Either ~> (,) = forall a b. Either a b -> (a, b) StateT ~> ReaderT = forall s m a. StateT s m a -> ReaderT s m a
We can of course define identity and composition for these, and it will be handy to do so:
class Morph (p :: k -> k -> *) where id :: p a a (.) :: p b c -> p a b -> p a c instance Morph (->) where id x = x (g . f) x = g (f x) instance Morph ((~>) :: k -> k -> *) => Morph (Transformer :: (i -> k) -> (i -> k) -> *) where id = Transform id Transform f . Transform g = Transform $ f . g
These categories can be looked upon as the most basic substrates in Haskell. For instance, every type of kind * -> * is an object of the relevant category, even if it's a GADT or has other structure that prevents it from being nicely functorial.
The category for * is of course just the normal category of types and functions we usually call Hask, and it is fairly analogous to the category of sets. One common activity in category theory is to study categories of sets equipped with extra structure, and it turns out we can do this in Haskell, as well. And it even makes some sense to study categories of structures over any of these type categories.
When we equip our types with structure, we often use type classes, so that's how I'll do things here. Classes have a special status socially in that we expect people to only define instances that adhere to certain equational rules. This will take the place of equations that we are not able to state in the Haskell type system, because it doesn't have dependent types. So using classes will allow us to define more structures that we normally would, if only by convention.
So, if we have a kind k, then a corresponding structure will be σ :: k -> Constraint. We can then define the category (k,σ) as having objects t :: k such that there is an instance σ t. Arrows are then taken to be f :: t ~> u such that f "respects" the operations of σ.
As a simple example, we have:
k = * σ = Monoid :: * -> Constraint Sum Integer, Product Integer, [Integer] :: (*, Monoid) f :: (Monoid m, Monoid n) => m -> n if f mempty = mempty f (m <> n) = f m <> f n
This is just the category of monoids in Haskell.
As a side note, we will sometimes be wanting to quantify over these "categories of structures". There isn't really a good way to package together a kind and a structure such that they work as a unit, but we can just add a constraint to the quantification. So, to quantify over all Monoids, we'll use 'forall m. Monoid m => ...'.
Now, once we have these categories of structures, there is an obvious forgetful functor back into the unadorned category. We can then look for free and cofree functors as adjoints to this. More symbolically:
Forget σ :: (k,σ) -> k Free σ :: k -> (k,σ) Cofree σ :: k -> (k,σ) Free σ ⊣ Forget σ ⊣ Cofree σ
However, what would be nicer (for some purposes) than having to look for these is being able to construct them all systematically, without having to think much about the structure σ.
Category theory gives a hint at this, too, in the form of Kan extensions. In category terms they look like:
p : C -> C' f : C -> D Ran p f : C' -> D Lan p f : C' -> D Ran p f c' = end (c : C). Hom_C'(c', p c) ⇒ f c Lan p f c' = coend (c : c). Hom_C'(p c, c') ⊗ f c
where ⇒ is a "power" and ⊗ is a copower, which are like being able to take exponentials and products by sets (or whatever the objects of the hom category are), instead of other objects within the category. Ends and coends are like universal and existential quantifiers (as are limits and colimits, but ends and coends involve mixed-variance).
Some handy theorems relate Kan extensions and adjoint functors:
if L ⊣ R then L = Ran R Id and R = Lan L Id if Ran R Id exists and is absolute then Ran R Id ⊣ R if Lan L Id exists and is absolute then L ⊣ Lan L Id Kan P F is absolute iff forall G. (G . Kan P F) ~= Kan P (G . F)
It turns out we can write down Kan extensions fairly generally in Haskell. Our restricted case is:
p = Forget σ :: (k,σ) -> k f = Id :: (k,σ) -> (k,σ) Free σ = Ran (Forget σ) Id :: k -> (k,σ) Cofree σ = Lan (Forget σ) Id :: k -> (k,σ) g :: (k,σ) -> j g . Free σ = Ran (Forget σ) g g . Cofree σ = Lan (Forget σ) g
As long as the final category is like one of our type constructor categories, ends are universal quantifiers, powers are function types, coends are existential quantifiers and copowers are product spaces. This only breaks down for our purposes when g is contravariant, in which case they are flipped. For higher kinds, these constructions occur point-wise. So, we can break things down into four general cases, each with cases for each arity:
newtype Ran0 σ p (f :: k -> *) a = Ran0 { ran0 :: forall r. σ r => (a ~> p r) -> f r } newtype Ran1 σ p (f :: k -> j -> *) a b = Ran1 { ran1 :: forall r. σ r => (a ~> p r) -> f r b } -- ... data RanOp0 σ p (f :: k -> *) a = forall e. σ e => RanOp0 (a ~> p e) (f e) -- ... data Lan0 σ p (f :: k -> *) a = forall e. σ e => Lan0 (p e ~> a) (f e) data Lan1 σ p (f :: k -> j -> *) a b = forall e. σ e => Lan1 (p e ~> a) (f e b) -- ... data LanOp0 σ p (f :: k -> *) a = LanOp0 { lan0 :: forall r. σ r => (p r -> a) -> f r } -- ...
The more specific proposed (co)free definitions are:
type family Free :: (k -> Constraint) -> k -> k type family Cofree :: (k -> Constraint) -> k -> k newtype Free0 σ a = Free0 { gratis0 :: forall r. σ r => (a ~> r) -> r } type instance Free = Free0 newtype Free1 σ f a = Free1 { gratis1 :: forall g. σ g => (f ~> g) -> g a } type instance Free = Free1 -- ... data Cofree0 σ a = forall e. σ e => Cofree0 (e ~> a) e type instance Cofree = Cofree0 data Cofree1 σ f a = forall g. σ g => Cofree1 (g ~> f) (g a) type instance Cofree = Cofree1 -- ...
We can define some handly classes and instances for working with these types, several of which generalize existing Haskell concepts:
class Covariant (f :: i -> j) where comap :: (a ~> b) -> (f a ~> f b) class Contravariant f where contramap :: (b ~> a) -> (f a ~> f b) class Covariant m => Monad (m :: i -> i) where pure :: a ~> m a join :: m (m a) ~> m a class Covariant w => Comonad (w :: i -> i) where extract :: w a ~> a split :: w a ~> w (w a) class Couniversal σ f | f -> σ where couniversal :: σ r => (a ~> r) -> (f a ~> r) class Universal σ f | f -> σ where universal :: σ e => (e ~> a) -> (e ~> f a) instance Covariant (Free0 σ) where comap f (Free0 e) = Free0 (e . (.f)) instance Monad (Free0 σ) where pure x = Free0 $ \k -> k x join (Free0 e) = Free0 $ \k -> e $ \(Free0 e) -> e k instance Couniversal σ (Free0 σ) where couniversal h (Free0 e) = e h -- ...
The only unfamiliar classes here should be (Co)Universal. They are for witnessing the adjunctions that make Free σ the initial σ and Cofree σ the final σ in the relevant way. Only one direction is given, since the opposite is very easy to construct with the (co)monad structure.
Free σ is a monad and couniversal, Cofree σ is a comonad and universal.
We can now try to convince ourselves that Free σ and Cofree σ are absolute Here are some examples:
free0Absolute0 :: forall g σ a. (Covariant g, σ (Free σ a)) => g (Free0 σ a) < -> Ran σ Forget g a free0Absolute0 = (l, r) where l :: g (Free σ a) -> Ran σ Forget g a l g = Ran0 $ \k -> comap (couniversal $ remember0 . k) g r :: Ran σ Forget g a -> g (Free σ a) r (Ran0 e) = e $ Forget0 . pure free0Absolute1 :: forall (g :: * -> * -> *) σ a x. (Covariant g, σ (Free σ a)) => g (Free0 σ a) x < -> Ran σ Forget g a x free0Absolute1 = (l, r) where l :: g (Free σ a) x -> Ran σ Forget g a x l g = Ran1 $ \k -> comap (couniversal $ remember0 . k) $$ g r :: Ran σ Forget g a x -> g (Free σ a) x r (Ran1 e) = e $ Forget0 . pure free0Absolute0Op :: forall g σ a. (Contravariant g, σ (Free σ a)) => g (Free0 σ a) < -> RanOp σ Forget g a free0Absolute0Op = (l, r) where l :: g (Free σ a) -> RanOp σ Forget g a l = RanOp0 $ Forget0 . pure r :: RanOp σ Forget g a -> g (Free σ a) r (RanOp0 h g) = contramap (couniversal $ remember0 . h) g -- ...
As can be seen, the definitions share a lot of structure. I'm quite confident that with the right building blocks these could be defined once for each of the four types of Kan extensions, with types like:
freeAbsolute :: forall g σ a. (Covariant g, σ (Free σ a)) => g (Free σ a) < ~> Ran σ Forget g a cofreeAbsolute :: forall g σ a. (Covariant g, σ (Cofree σ a)) => g (Cofree σ a) < ~> Lan σ Forget g a freeAbsoluteOp :: forall g σ a. (Contravariant g, σ (Free σ a)) => g (Free σ a) < ~> RanOp σ Forget g a cofreeAbsoluteOp :: forall g σ a. (Contravariant g, σ (Cofree σ a)) => g (Cofree σ a) < ~> LanOp σ Forget g a
However, it seems quite difficult to structure things in a way such that GHC will accept the definitions. I've successfully written freeAbsolute using some axioms, but turning those axioms into class definitions and the like seems impossible.
Anyhow, the punchline is that we can prove absoluteness using only the premise that there is a valid σ instance for Free σ and Cofree σ. This tends to be quite easy; we just borrow the structure of the type we are quantifying over. This means that in all these cases, we are justified in saying that Free σ ⊣ Forget σ ⊣ Cofree σ, and we have a very generic presentations of (co)free structures in Haskell. So let's look at some.
We've already seen Free Monoid, and last time we talked about Free Applicative, and its relation to traversals. But, Applicative is to traversal as Functor is to lens, so it may be interesting to consider constructions on that. Both Free Functor and Cofree Functor make Functors:
instance Functor (Free1 Functor f) where fmap f (Free1 e) = Free1 $ fmap f . e instance Functor (Cofree1 Functor f) where fmap f (Cofree1 h e) = Cofree1 h (fmap f e)
And of course, they are (co)monads, covariant functors and (co)universal among Functors. But, it happens that I know some other types with these properties:
data CoYo f a = forall e. CoYo (e -> a) (f e) instance Covariant CoYo where comap f = Transform $ \(CoYo h e) -> CoYo h (f $$ e) instance Monad CoYo where pure = Transform $ CoYo id join = Transform $ \(CoYo h (CoYo h' e)) -> CoYo (h . h') e instance Functor (CoYo f) where fmap f (CoYo h e) = CoYo (f . h) e instance Couniversal Functor CoYo where couniversal tr = Transform $ \(CoYo h e) -> fmap h (tr $$ e) newtype Yo f a = Yo { oy :: forall r. (a -> r) -> f r } instance Covariant Yo where comap f = Transform $ \(Yo e) -> Yo $ (f $$) . e instance Comonad Yo where extract = Transform $ \(Yo e) -> e id split = Transform $ \(Yo e) -> Yo $ \k -> Yo $ \k' -> e $ k' . k instance Functor (Yo f) where fmap f (Yo e) = Yo $ \k -> e (k . f) instance Universal Functor Yo where universal tr = Transform $ \e -> Yo $ \k -> tr $$ fmap k e
These are the types involved in the (co-)Yoneda lemma. CoYo is a monad, couniversal among functors, and CoYo f is a Functor. Yo is a comonad, universal among functors, and is always a Functor. So, are these equivalent types?
coyoIso :: CoYo < ~> Free Functor coyoIso = (Transform $ couniversal pure, Transform $ couniversal pure) yoIso :: Yo < ~> Cofree Functor yoIso = (Transform $ universal extract, Transform $ universal extract)
Indeed they are. And similar identities hold for the contravariant versions of these constructions.
I don't have much of a use for this last example. I suppose to be perfectly precise, I should point out that these uses of (Co)Yo are not actually part of the (co-)Yoneda lemma. They are two different constructions. The (co-)Yoneda lemma can be given in terms of Kan extensions as:
yoneda :: Ran Id f < ~> f coyoneda :: Lan Id f < ~> f
But, the use of (Co)Yo to make Functors out of things that aren't necessarily is properly thought of in other terms. In short, we have some kind of category of Haskell types with only identity arrows---it is discrete. Then any type constructor, even non-functorial ones, is certainly a functor from said category (call it Haskrete) into the normal one (Hask). And there is an inclusion functor from Haskrete into Hask:
F
Haskrete -----> Hask
| /|
| /
| /
Incl | /
| / Ran/Lan Incl F
| /
| /
v /
Hask
So, (Co)Free Functor can also be thought of in terms of these Kan extensions involving the discrete category.
To see more fleshed out, loadable versions of the code in this post, see this file. I may also try a similar Agda development at a later date, as it may admit the more general absoluteness constructions easier.
[0]: The reason for restricting ourselves to kinds involving only * and (->) is that they work much more simply than data kinds. Haskell values can't depend on type-level entities without using type classes. For *, this is natural, but for something like Bool -> *, it is more natural for transformations to be able to inspect the booleans, and so should be something more like forall b. InspectBool b => f b -> g b.
[1]: First-class types are what you get by removing type families and synonyms from consideration. The reason for doing so is that these can't be used properly as parameters and the like, except in cases where they reduce to some other type that is first-class. For example, if we define:
type I a = a
even though GHC will report I :: * -> *, it is not legal to write Transform I I.

 and
and  , a functor
, a functor 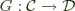 , and provided some conditions in
, and provided some conditions in  , the codensity monad of
, the codensity monad of 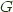 .
.![$ T^G(a) = \int_r \left[\mathcal{D}(a, Gr), Gr\right] $ $ T^G(a) = \int_r \left[\mathcal{D}(a, Gr), Gr\right] $](http://comonad.com/latex/050bb5034bed82159df4c52c89c07f3c.png)
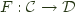 , and
, and 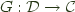 and a natural isomorphism:
and a natural isomorphism: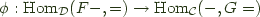
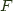 the left adjoint functor, and
the left adjoint functor, and 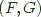 an adjoint pair, and write this relationship as
an adjoint pair, and write this relationship as 