The Comonad.Reader

A common occurrence in category theory is the adjoint triple. This is a pair of adjunctions relating three functors:

F ⊣ G ⊣ H
F ⊣ G, G ⊣ H

Perhaps part of the reason they are so common is that (co)limits form one:

colim ⊣ Δ ⊣ lim

where Δ : C -> C^J is the diagonal functor, which takes objects in C to the constant functor returning that object. A version of this shows up in Haskell (with some extensions) and dependent type theories, as:

∃ ⊣ Const ⊣ ∀
Σ ⊣ Const ⊣ Π

where, if we only care about quantifying over a single variable, existential and sigma types can be seen as a left adjoint to a diagonal functor that maps types into constant type families (either over * for the first triple in Haskell, or some other type for the second in a dependently typed language), while universal and pi types can be seen as a right adjoint to the same.

It's not uncommon to see the above information in type theory discussion forums. But, there are a few cute properties and examples of adjoint triples that I haven't really seen come up in such contexts.

To begin, we can compose the two adjunctions involved, since the common functor ensures things match up. By calculating on the hom definition, we can see:

Hom(FGA, B)     Hom(GFA, B)
    ~=              ~=
Hom(GA, GB)     Hom(FA, HB)
    ~=              ~=
Hom(A, HGB)     Hom(A, GHB)

So there are two ways to compose the adjunctions, giving two induced adjunctions:

FG ⊣ HG,  GF ⊣ GH

And there is something special about these adjunctions. Note that FG is the comonad for the F ⊣ G adjunction, while HG is the monad for the G ⊣ H adjunction. Similarly, GF is the F ⊣ G monad, and GH is the G ⊣ H comonad. So each adjoint triple gives rise to two adjunctions between monads and comonads.

The second of these has another interesting property. We often want to consider the algebras of a monad, and coalgebras of a comonad. The (co)algebra operations with carrier A have type:

alg   : GFA -> A
coalg : A -> GHA

but these types are isomorphic according to the GF ⊣ GH adjunction. Thus, one might guess that GF monad algebras are also GH comonad coalgebras, and that in such a situation, we actually have some structure that can be characterized both ways. In fact this is true for any monad left adjoint to a comonad; [0] but all adjoint triples give rise to these.

The first adjunction actually turns out to be more familiar for the triple examples above, though. (Edit: [2]) If we consider the Σ ⊣ Const ⊣ Π adjunction, where:

Σ Π : (A -> Type) -> Type
Const : Type -> (A -> Type)

we get:

ΣConst : Type -> Type
ΣConst B = A × B
ΠConst : Type -> Type
ΠConst B = A -> B

So this is the familiar adjunction:

A × - ⊣ A -> -

But, there happens to be a triple that is a bit more interesting for both cases. It refers back to categories of functors vs. bare type constructors mentioned in previous posts. So, suppose we have a category called Con whose objects are (partially applied) type constructors (f, g) with kind * -> *, and arrows are polymorphic functions with types like:

 
forall x. f x -> g x
 

And let us further imagine that there is a similar category, called Func, except its objects are the things with Functor instances. Now, there is a functor:

U : Func -> Con

that 'forgets' the functor instance requirement. This functor is in the middle of an adjoint triple:

F ⊣ U ⊣ C
F, C : Con -> Func

where F creates the free functor over a type constructor, and C creates the cofree functor over a type constructor. These can be written using the types:

 
data F f a = forall e. F (e -> a) (f e)
newtype C f a = C (forall r. (a -> r) -> f r)
 

and these types will also serve as the types involved in the composite adjunctions:

FU ⊣ CU : Func -> Func
UF ⊣ UC : Con -> Con

Now, CU is a monad on functors, and the Yoneda lemma tells us that it is actually the identity monad. Similarly, FU is a comonad, and the co-Yoneda lemma tells us that it is the identity comonad (which makes sense, because identity is self-adjoint; and the above is why F and C are often named (Co)Yoneda in Haskell examples).

On the other hand, UF is a monad on type constructors (note, U isn't represented in the Haskell types; F and C just play triple duty, and the constraints on f control what's going on):

 
eta :: f a -> F f a
eta = F id
 
transform :: (forall x. f x -> g x) -> F f a -> F g a
transform tr (F g x) = F g (tr x)
 
mu :: F (F f) a -> F f a
mu (F g (F h x)) = F (g . h) x
 

and UC is a comonad:

 
epsilon :: C f a -> f a
epsilon (C e) = e id
 
transform' :: (forall x. f x -> g x) -> C f a -> C g a
transform' tr (C e) = C (tr . e)
 
delta :: C f a -> C (C f) a
delta (C e) = C $ \h -> C $ \g -> e (g . h)
 

These are not the identity (co)monad, but this is the case where we have algebras and coalgebras that are equivalent. So, what are the (co)algebras? If we consider UF (and unpack the definitions somewhat):

 
alg :: forall e. (e -> a, f e) -> f a
alg (id, x) = x
alg (g . h, x) = alg (g, alg (h, x))
 

and for UC:

 
coalg :: f a -> forall r. (a -> r) -> f r
coalg x id = x
coalg x (g . h) = coalg (coalg x h) g
 

in other words, (co)algebra actions of these (co)monads are (mangled) fmap implementations, and the commutativity requirements are exactly what is required to be a law abiding instance. So the (co)algebras are exactly the Functors. [1]

There are, of course, many other examples of adjoint triples. And further, there are even adjoint quadruples, which in turn give rise to adjoint triples of (co)monads. Hopefully this has sparked some folks' interest in finding and studying more interesting examples.

[0]: Another exmaple is A × - ⊣ A -> - where the A in question is a monoid. (Co)monad (co)algebras of these correspond to actions of the monoid on the carrier set.

[1]: This shouldn't be too surprising, because having a category of (co)algebraic structures that is equivalent to the category of (co)algebras of the (co)monad that comes from the (co)free-forgetful adjunction is the basis for doing algebra in category theory (with (co)monads, at least). However, it is somewhat unusual for a forgetful functor to have both a left and right adjoint. In many cases, something is either algebraic or coalgebraic, and not both.

[2]: Urs Schreiber informed me of an interesting interpretation of the ConstΣ ⊣ ConstΠ adjunction. If you are familiar with modal logic and the possible worlds semantics thereof, you can probably imagine that we could model it using something like P : W -> Type, where W is the type of possible worlds, and propositions are types. Then values of type Σ P demonstrate that P holds in particular worlds, while values of type Π P demonstrate that it holds in all worlds. Const turns these types back into world-indexed 'propositions,' so ConstΣ is the possibility modality and ConstΠ is the necessity modality.

In the last couple posts I've used some 'free' constructions, and not remarked too much on how they arise. In this post, I'd like to explore them more. This is going to be something of a departure from the previous posts, though, since I'm not going to worry about thinking precisely about bottom/domains. This is more an exercise in applying some category theory to Haskell, "fast and loose".

(Advance note: for some continuous code to look at see this file.)

First, it'll help to talk about how some categories can work in Haskell. For any kind k made of * and (->), [0] we can define a category of type constructors. Objects of the category will be first-class [1] types of that kind, and arrows will be defined by the following type family:

 
newtype Transformer f g = Transform { ($$) :: forall i. f i ~> g i }
 
type family (~>) :: k -> k -> * where
  (~>) = (->)
  (~>) = Transformer
 
type a < -> b = (a -> b, b -> a)
type a < ~> b = (a ~> b, b ~> a)
 

So, for a base case, * has monomorphic functions as arrows, and categories for higher kinds have polymorphic functions that saturate the constructor:

 
  Int ~> Char = Int -> Char
  Maybe ~> [] = forall a. Maybe a -> [a]
  Either ~> (,) = forall a b. Either a b -> (a, b)
  StateT ~> ReaderT = forall s m a. StateT s m a -> ReaderT s m a
 

We can of course define identity and composition for these, and it will be handy to do so:

 
class Morph (p :: k -> k -> *) where
  id :: p a a
  (.) :: p b c -> p a b -> p a c
 
instance Morph (->) where
  id x = x
  (g . f) x = g (f x)
 
instance Morph ((~>) :: k -> k -> *)
      => Morph (Transformer :: (i -> k) -> (i -> k) -> *) where
  id = Transform id
  Transform f . Transform g = Transform $ f . g
 

These categories can be looked upon as the most basic substrates in Haskell. For instance, every type of kind * -> * is an object of the relevant category, even if it's a GADT or has other structure that prevents it from being nicely functorial.

The category for * is of course just the normal category of types and functions we usually call Hask, and it is fairly analogous to the category of sets. One common activity in category theory is to study categories of sets equipped with extra structure, and it turns out we can do this in Haskell, as well. And it even makes some sense to study categories of structures over any of these type categories.

When we equip our types with structure, we often use type classes, so that's how I'll do things here. Classes have a special status socially in that we expect people to only define instances that adhere to certain equational rules. This will take the place of equations that we are not able to state in the Haskell type system, because it doesn't have dependent types. So using classes will allow us to define more structures that we normally would, if only by convention.

So, if we have a kind k, then a corresponding structure will be σ :: k -> Constraint. We can then define the category (k,σ) as having objects t :: k such that there is an instance σ t. Arrows are then taken to be f :: t ~> u such that f "respects" the operations of σ.

As a simple example, we have:

 
  k = *
  σ = Monoid :: * -> Constraint
 
  Sum Integer, Product Integer, [Integer] :: (*, Monoid)
 
  f :: (Monoid m, Monoid n) => m -> n
    if f mempty = mempty
       f (m <> n) = f m <> f n
 

This is just the category of monoids in Haskell.

As a side note, we will sometimes be wanting to quantify over these "categories of structures". There isn't really a good way to package together a kind and a structure such that they work as a unit, but we can just add a constraint to the quantification. So, to quantify over all Monoids, we'll use 'forall m. Monoid m => ...'.

Now, once we have these categories of structures, there is an obvious forgetful functor back into the unadorned category. We can then look for free and cofree functors as adjoints to this. More symbolically:

 
  Forget σ :: (k,σ) -> k
  Free   σ :: k -> (k,σ)
  Cofree σ :: k -> (k,σ)
 
  Free σ ⊣ Forget σ ⊣ Cofree σ
 

However, what would be nicer (for some purposes) than having to look for these is being able to construct them all systematically, without having to think much about the structure σ.

Category theory gives a hint at this, too, in the form of Kan extensions. In category terms they look like:

  p : C -> C'
  f : C -> D
  Ran p f : C' -> D
  Lan p f : C' -> D

  Ran p f c' = end (c : C). Hom_C'(c', p c) ⇒ f c
  Lan p f c' = coend (c : c). Hom_C'(p c, c') ⊗ f c

where ⇒ is a "power" and ⊗ is a copower, which are like being able to take exponentials and products by sets (or whatever the objects of the hom category are), instead of other objects within the category. Ends and coends are like universal and existential quantifiers (as are limits and colimits, but ends and coends involve mixed-variance).

Some handy theorems relate Kan extensions and adjoint functors:

  if L ⊣ R
  then L = Ran R Id and R = Lan L Id

  if Ran R Id exists and is absolute
  then Ran R Id ⊣ R

  if Lan L Id exists and is absolute
  then L ⊣ Lan L Id

  Kan P F is absolute iff forall G. (G . Kan P F) ~= Kan P (G . F)

It turns out we can write down Kan extensions fairly generally in Haskell. Our restricted case is:

 
  p = Forget σ :: (k,σ) -> k
  f = Id :: (k,σ) -> (k,σ)
 
  Free   σ = Ran (Forget σ) Id :: k -> (k,σ)
  Cofree σ = Lan (Forget σ) Id :: k -> (k,σ)
 
  g :: (k,σ) -> j
  g . Free   σ = Ran (Forget σ) g
  g . Cofree σ = Lan (Forget σ) g
 

As long as the final category is like one of our type constructor categories, ends are universal quantifiers, powers are function types, coends are existential quantifiers and copowers are product spaces. This only breaks down for our purposes when g is contravariant, in which case they are flipped. For higher kinds, these constructions occur point-wise. So, we can break things down into four general cases, each with cases for each arity:

 
newtype Ran0 σ p (f :: k -> *) a =
  Ran0 { ran0 :: forall r. σ r => (a ~> p r) -> f r }
 
newtype Ran1 σ p (f :: k -> j -> *) a b =
  Ran1 { ran1 :: forall r. σ r => (a ~> p r) -> f r b }
 
-- ...
 
data RanOp0 σ p (f :: k -> *) a =
  forall e. σ e => RanOp0 (a ~> p e) (f e)
 
-- ...
 
data Lan0 σ p (f :: k -> *) a =
  forall e. σ e => Lan0 (p e ~> a) (f e)
 
data Lan1 σ p (f :: k -> j -> *) a b =
  forall e. σ e => Lan1 (p e ~> a) (f e b)
 
-- ...
 
data LanOp0 σ p (f :: k -> *) a =
  LanOp0 { lan0 :: forall r. σ r => (p r -> a) -> f r }
 
-- ...
 

The more specific proposed (co)free definitions are:

 
type family Free   :: (k -> Constraint) -> k -> k
type family Cofree :: (k -> Constraint) -> k -> k
 
newtype Free0 σ a = Free0 { gratis0 :: forall r. σ r => (a ~> r) -> r }
type instance Free = Free0
 
newtype Free1 σ f a = Free1 { gratis1 :: forall g. σ g => (f ~> g) -> g a }
type instance Free = Free1
 
-- ...
 
data Cofree0 σ a = forall e. σ e => Cofree0 (e ~> a) e
type instance Cofree = Cofree0
 
data Cofree1 σ f a = forall g. σ g => Cofree1 (g ~> f) (g a)
type instance Cofree = Cofree1
 
-- ...
 

We can define some handly classes and instances for working with these types, several of which generalize existing Haskell concepts:

 
class Covariant (f :: i -> j) where
  comap :: (a ~> b) -> (f a ~> f b)
 
class Contravariant f where
  contramap :: (b ~> a) -> (f a ~> f b)
 
class Covariant m => Monad (m :: i -> i) where
  pure :: a ~> m a
  join :: m (m a) ~> m a
 
class Covariant w => Comonad (w :: i -> i) where
  extract :: w a ~> a
  split :: w a ~> w (w a)
 
class Couniversal σ f | f -> σ where
  couniversal :: σ r => (a ~> r) -> (f a ~> r)
 
class Universal σ f | f -> σ where
  universal :: σ e => (e ~> a) -> (e ~> f a)
 
instance Covariant (Free0 σ) where
  comap f (Free0 e) = Free0 (e . (.f))
 
instance Monad (Free0 σ) where
  pure x = Free0 $ \k -> k x
  join (Free0 e) = Free0 $ \k -> e $ \(Free0 e) -> e k
 
instance Couniversal σ (Free0 σ) where
  couniversal h (Free0 e) = e h
 
-- ...
 

The only unfamiliar classes here should be (Co)Universal. They are for witnessing the adjunctions that make Free σ the initial σ and Cofree σ the final σ in the relevant way. Only one direction is given, since the opposite is very easy to construct with the (co)monad structure.

Free σ is a monad and couniversal, Cofree σ is a comonad and universal.

We can now try to convince ourselves that Free σ and Cofree σ are absolute Here are some examples:

 
free0Absolute0 :: forall g σ a. (Covariant g, σ (Free σ a))
               => g (Free0 σ a) < -> Ran σ Forget g a
free0Absolute0 = (l, r)
 where
 l :: g (Free σ a) -> Ran σ Forget g a
 l g = Ran0 $ \k -> comap (couniversal $ remember0 . k) g
 
 r :: Ran σ Forget g a -> g (Free σ a)
 r (Ran0 e) = e $ Forget0 . pure
 
free0Absolute1 :: forall (g :: * -> * -> *) σ a x. (Covariant g, σ (Free σ a))
               => g (Free0 σ a) x < -> Ran σ Forget g a x
free0Absolute1 = (l, r)
 where
 l :: g (Free σ a) x -> Ran σ Forget g a x
 l g = Ran1 $ \k -> comap (couniversal $ remember0 . k) $$ g
 
 r :: Ran σ Forget g a x -> g (Free σ a) x
 r (Ran1 e) = e $ Forget0 . pure
 
free0Absolute0Op :: forall g σ a. (Contravariant g, σ (Free σ a))
                 => g (Free0 σ a) < -> RanOp σ Forget g a
free0Absolute0Op = (l, r)
 where
 l :: g (Free σ a) -> RanOp σ Forget g a
 l = RanOp0 $ Forget0 . pure
 
 r :: RanOp σ Forget g a -> g (Free σ a)
 r (RanOp0 h g) = contramap (couniversal $ remember0 . h) g
 
-- ...
 

As can be seen, the definitions share a lot of structure. I'm quite confident that with the right building blocks these could be defined once for each of the four types of Kan extensions, with types like:

 
freeAbsolute
  :: forall g σ a. (Covariant g, σ (Free σ a))
  => g (Free σ a) < ~> Ran σ Forget g a
 
cofreeAbsolute
  :: forall g σ a. (Covariant g, σ (Cofree σ a))
  => g (Cofree σ a) < ~> Lan σ Forget g a
 
freeAbsoluteOp
  :: forall g σ a. (Contravariant g, σ (Free σ a))
  => g (Free σ a) < ~> RanOp σ Forget g a
 
cofreeAbsoluteOp
  :: forall g σ a. (Contravariant g, σ (Cofree σ a))
  => g (Cofree σ a) < ~> LanOp σ Forget g a
 

However, it seems quite difficult to structure things in a way such that GHC will accept the definitions. I've successfully written freeAbsolute using some axioms, but turning those axioms into class definitions and the like seems impossible.

Anyhow, the punchline is that we can prove absoluteness using only the premise that there is a valid σ instance for Free σ and Cofree σ. This tends to be quite easy; we just borrow the structure of the type we are quantifying over. This means that in all these cases, we are justified in saying that Free σ ⊣ Forget σ ⊣ Cofree σ, and we have a very generic presentations of (co)free structures in Haskell. So let's look at some.

We've already seen Free Monoid, and last time we talked about Free Applicative, and its relation to traversals. But, Applicative is to traversal as Functor is to lens, so it may be interesting to consider constructions on that. Both Free Functor and Cofree Functor make Functors:

 
instance Functor (Free1 Functor f) where
  fmap f (Free1 e) = Free1 $ fmap f . e
 
instance Functor (Cofree1 Functor f) where
  fmap f (Cofree1 h e) = Cofree1 h (fmap f e)
 

And of course, they are (co)monads, covariant functors and (co)universal among Functors. But, it happens that I know some other types with these properties:

 
data CoYo f a = forall e. CoYo (e -> a) (f e)
 
instance Covariant CoYo where
  comap f = Transform $ \(CoYo h e) -> CoYo h (f $$ e)
 
instance Monad CoYo where
  pure = Transform $ CoYo id
  join = Transform $ \(CoYo h (CoYo h' e)) -> CoYo (h . h') e
 
instance Functor (CoYo f) where
  fmap f (CoYo h e) = CoYo (f . h) e
 
instance Couniversal Functor CoYo where
  couniversal tr = Transform $ \(CoYo h e) -> fmap h (tr $$ e)
 
newtype Yo f a = Yo { oy :: forall r. (a -> r) -> f r }
 
instance Covariant Yo where
  comap f = Transform $ \(Yo e) -> Yo $ (f $$) . e
 
instance Comonad Yo where
  extract = Transform $ \(Yo e) -> e id
  split = Transform $ \(Yo e) -> Yo $ \k -> Yo $ \k' -> e $ k' . k
 
instance Functor (Yo f) where
  fmap f (Yo e) = Yo $ \k -> e (k . f)
 
instance Universal Functor Yo where
  universal tr = Transform $ \e -> Yo $ \k -> tr $$ fmap k e
 

These are the types involved in the (co-)Yoneda lemma. CoYo is a monad, couniversal among functors, and CoYo f is a Functor. Yo is a comonad, universal among functors, and is always a Functor. So, are these equivalent types?

 
coyoIso :: CoYo < ~> Free Functor
coyoIso = (Transform $ couniversal pure, Transform $ couniversal pure)
 
yoIso :: Yo < ~> Cofree Functor
yoIso = (Transform $ universal extract, Transform $ universal extract)
 

Indeed they are. And similar identities hold for the contravariant versions of these constructions.

I don't have much of a use for this last example. I suppose to be perfectly precise, I should point out that these uses of (Co)Yo are not actually part of the (co-)Yoneda lemma. They are two different constructions. The (co-)Yoneda lemma can be given in terms of Kan extensions as:

 
yoneda :: Ran Id f < ~> f
 
coyoneda :: Lan Id f < ~> f
 

But, the use of (Co)Yo to make Functors out of things that aren't necessarily is properly thought of in other terms. In short, we have some kind of category of Haskell types with only identity arrows---it is discrete. Then any type constructor, even non-functorial ones, is certainly a functor from said category (call it Haskrete) into the normal one (Hask). And there is an inclusion functor from Haskrete into Hask:

             F
 Haskrete -----> Hask
      |        /|
      |       /
      |      /
Incl  |     /
      |    /  Ran/Lan Incl F
      |   /
      |  /
      v /
    Hask

So, (Co)Free Functor can also be thought of in terms of these Kan extensions involving the discrete category.

To see more fleshed out, loadable versions of the code in this post, see this file. I may also try a similar Agda development at a later date, as it may admit the more general absoluteness constructions easier.

[0]: The reason for restricting ourselves to kinds involving only * and (->) is that they work much more simply than data kinds. Haskell values can't depend on type-level entities without using type classes. For *, this is natural, but for something like Bool -> *, it is more natural for transformations to be able to inspect the booleans, and so should be something more like forall b. InspectBool b => f b -> g b.

[1]: First-class types are what you get by removing type families and synonyms from consideration. The reason for doing so is that these can't be used properly as parameters and the like, except in cases where they reduce to some other type that is first-class. For example, if we define:

 
type I a = a
 

even though GHC will report I :: * -> *, it is not legal to write Transform I I.

Last time I looked at free monoids, and noticed that in Haskell lists don't really cut it. This is a consequence of laziness and general recursion. To model a language with those properties, one needs to use domains and monotone, continuous maps, rather than sets and total functions (a call-by-value language with general recursion would use domains and strict maps instead).

This time I'd like to talk about some other examples of this, and point out how doing so can (perhaps) resolve some disagreements that people have about the specific cases.

The first example is not one that I came up with: induction. It's sometimes said that Haskell does not have inductive types at all, or that we cannot reason about functions on its data types by induction. However, I think this is (techincally) inaccurate. What's true is that we cannot simply pretend that that our types are sets and use the induction principles for sets to reason about Haskell programs. Instead, one has to figure out what inductive domains would be, and what their proof principles are.

Fortunately, there are some papers about doing this. The most recent (that I'm aware of) is Generic Fibrational Induction. I won't get too into the details, but it shows how one can talk about induction in a general setting, where one has a category that roughly corresponds to the type theory/programming language, and a second category of proofs that is 'indexed' by the first category's objects. Importantly, it is not required that the second category is somehow 'part of' the type theory being reasoned about, as is often the case with dependent types, although that is also a special case of their construction.

One of the results of the paper is that this framework can be used to talk about induction principles for types that don't make sense as sets. Specifically:

 
newtype Hyp = Hyp ((Hyp -> Int) -> Int)
 

the type of "hyperfunctions". Instead of interpreting this type as a set, where it would effectively require a set that is isomorphic to the power set of its power set, they interpret it in the category of domains and strict functions mentioned earlier. They then construct the proof category in a similar way as one would for sets, except instead of talking about predicates as subsets, we talk about sub-domains instead. Once this is done, their framework gives a notion of induction for this type.

This example is suitable for ML (and suchlike), due to the strict functions, and sort of breaks the idea that we can really get away with only thinking about sets, even there. Sets are good enough for some simple examples (like flat domains where we don't care about ⊥), but in general we have to generalize induction itself to apply to all types in the 'good' language.

While I haven't worked out how the generic induction would work out for Haskell, I have little doubt that it would, because ML actually contains all of Haskell's data types (and vice versa). So the fact that the framework gives meaning to induction for ML implies that it does so for Haskell. If one wants to know what induction for Haskell's 'lazy naturals' looks like, they can study the ML analogue of:

 
data LNat = Zero | Succ (() -> LNat)
 

because function spaces lift their codomain, and make things 'lazy'.

----

The other example I'd like to talk about hearkens back to the previous article. I explained how foldMap is the proper fundamental method of the Foldable class, because it can be massaged to look like:

 
foldMap :: Foldable f => f a -> FreeMonoid a
 

and lists are not the free monoid, because they do not work properly for various infinite cases.

I also mentioned that foldMap looks a lot like traverse:

 
foldMap  :: (Foldable t   , Monoid m)      => (a -> m)   -> t a -> m
traverse :: (Traversable t, Applicative f) => (a -> f b) -> t a -> f (t b)
 

And of course, we have Monoid m => Applicative (Const m), and the functions are expected to agree in this way when applicable.

Now, people like to get in arguments about whether traversals are allowed to be infinite. I know Ed Kmett likes to argue that they can be, because he has lots of examples. But, not everyone agrees, and especially people who have papers proving things about traversals tend to side with the finite-only side. I've heard this includes one of the inventors of Traversable, Conor McBride.

In my opinion, the above disagreement is just another example of a situation where we have a generic notion instantiated in two different ways, and intuition about one does not quite transfer to the other. If you are working in a language like Agda or Coq (for proving), you will be thinking about traversals in the context of sets and total functions. And there, traversals are finite. But in Haskell, there are infinitary cases to consider, and they should work out all right when thinking about domains instead of sets. But I should probably put forward some argument for this position (and even if I don't need to, it leads somewhere else interesting).

One example that people like to give about finitary traversals is that they can be done via lists. Given a finite traversal, we can traverse to get the elements (using Const [a]), traverse the list, then put them back where we got them by traversing again (using State [a]). Usually when you see this, though, there's some subtle cheating in relying on the list to be exactly the right length for the second traversal. It will be, because we got it from a traversal of the same structure, but I would expect that proving the function is actually total to be a lot of work. Thus, I'll use this as an excuse to do my own cheating later.

Now, the above uses lists, but why are we using lists when we're in Haskell? We know they're deficient in certain ways. It turns out that we can give a lot of the same relevant structure to the better free monoid type:

 
newtype FM a = FM (forall m. Monoid m => (a -> m) -> m) deriving (Functor)
 
instance Applicative FM where
  pure x = FM ($ x)
  FM ef < *> FM ex = FM $ \k -> ef $ \f -> ex $ \x -> k (f x)
 
instance Monoid (FM a) where
  mempty = FM $ \_ -> mempty
  mappend (FM l) (FM r) = FM $ \k -> l k <> r k
 
instance Foldable FM where
  foldMap f (FM e) = e f
 
newtype Ap f b = Ap { unAp :: f b }
 
instance (Applicative f, Monoid b) => Monoid (Ap f b) where
  mempty = Ap $ pure mempty
  mappend (Ap l) (Ap r) = Ap $ (<>) < $> l < *> r
 
instance Traversable FM where
  traverse f (FM e) = unAp . e $ Ap . fmap pure . f
 

So, free monoids are Monoids (of course), Foldable, and even Traversable. At least, we can define something with the right type that wouldn't bother anyone if it were written in a total language with the right features, but in Haskell it happens to allow various infinite things that people don't like.

Now it's time to cheat. First, let's define a function that can take any Traversable to our free monoid:

 
toFreeMonoid :: Traversable t => t a -> FM a
toFreeMonoid f = FM $ \k -> getConst $ traverse (Const . k) f
 

Now let's define a Monoid that's not a monoid:

 
data Cheat a = Empty | Single a | Append (Cheat a) (Cheat a)
 
instance Monoid (Cheat a) where
  mempty = Empty
  mappend = Append
 

You may recognize this as the data version of the free monoid from the previous article, where we get the real free monoid by taking a quotient. using this, we can define an Applicative that's not valid:

 
newtype Cheating b a =
  Cheating { prosper :: Cheat b -> a } deriving (Functor)
 
instance Applicative (Cheating b) where
  pure x = Cheating $ \_ -> x
 
  Cheating f < *> Cheating x = Cheating $ \c -> case c of
    Append l r -> f l (x r)
 

Given these building blocks, we can define a function to relabel a traversable using a free monoid:

 
relabel :: Traversable t => t a -> FM b -> t b
relabel t (FM m) = propser (traverse (const hope) t) (m Single)
 where
 hope = Cheating $ \c -> case c of
   Single x -> x
 

And we can implement any traversal by taking a trip through the free monoid:

 
slowTraverse
  :: (Applicative f, Traversable t) => (a -> f b) -> t a -> f (t b)
slowTraverse f t = fmap (relabel t) . traverse f . toFreeMonoid $ t
 

And since we got our free monoid via traversing, all the partiality I hid in the above won't blow up in practice, rather like the case with lists and finite traversals.

Arguably, this is worse cheating. It relies on the exact association structure to work out, rather than just number of elements. The reason is that for infinitary cases, you cannot flatten things out, and there's really no way to detect when you have something infinitary. The finitary traversals have the luxury of being able to reassociate everything to a canonical form, while the infinite cases force us to not do any reassociating at all. So this might be somewhat unsatisfying.

But, what if we didn't have to cheat at all? We can get the free monoid by tweaking foldMap, and it looks like traverse, so what happens if we do the same manipulation to the latter?

It turns out that lens has a type for this purpose, a slight specialization of which is:

 
newtype Bazaar a b t =
  Bazaar { runBazaar :: forall f. Applicative f => (a -> f b) -> f t }
 

Using this type, we can reorder traverse to get:

 
howBizarre :: Traversable t => t a -> Bazaar a b (t b)
howBizarre t = Bazaar $ \k -> traverse k t
 

But now, what do we do with this? And what even is it? [1]

If we continue drawing on intuition from Foldable, we know that foldMap is related to the free monoid. Traversable has more indexing, and instead of Monoid uses Applicative. But the latter are actually related to the former; Applicatives are monoidal (closed) functors. And it turns out, Bazaar has to do with free Applicatives.

If we want to construct free Applicatives, we can use our universal property encoding trick:

 
newtype Free p f a =
  Free { gratis :: forall g. p g => (forall x. f x -> g x) -> g a }
 

This is a higher-order version of the free p, where we parameterize over the constraint we want to use to represent structures. So Free Applicative f is the free Applicative over a type constructor f. I'll leave the instances as an exercise.

Since free monoid is a monad, we'd expect Free p to be a monad, too. In this case, it is a McBride style indexed monad, as seen in The Kleisli Arrows of Outrageous Fortune.

 
type f ~> g = forall x. f x -> g x
 
embed :: f ~> Free p f
embed fx = Free $ \k -> k fx
 
translate :: (f ~> g) -> Free p f ~> Free p g
translate tr (Free e) = Free $ \k -> e (k . tr)
 
collapse :: Free p (Free p f) ~> Free p f
collapse (Free e) = Free $ \k -> e $ \(Free e') -> e' k
 

That paper explains how these are related to Atkey style indexed monads:

 
data At key i j where
  At :: key -> At key i i
 
type Atkey m i j a = m (At a j) i
 
ireturn :: IMonad m => a -> Atkey m i i a
ireturn = ...
 
ibind :: IMonad m => Atkey m i j a -> (a -> Atkey m j k b) -> Atkey m i k b
ibind = ...
 

It turns out, Bazaar is exactly the Atkey indexed monad derived from the Free Applicative indexed monad (with some arguments shuffled) [2]:

 
hence :: Bazaar a b t -> Atkey (Free Applicative) t b a
hence bz = Free $ \tr -> runBazaar bz $ tr . At
 
forth :: Atkey (Free Applicative) t b a -> Bazaar a b t
forth fa = Bazaar $ \g -> gratis fa $ \(At a) -> g a
 
imap :: (a -> b) -> Bazaar a i j -> Bazaar b i j
imap f (Bazaar e) = Bazaar $ \k -> e (k . f)
 
ipure :: a -> Bazaar a i i
ipure x = Bazaar ($ x)
 
(>>>=) :: Bazaar a j i -> (a -> Bazaar b k j) -> Bazaar b k i
Bazaar e >>>= f = Bazaar $ \k -> e $ \x -> runBazaar (f x) k
 
(>==>) :: (s -> Bazaar i o t) -> (i -> Bazaar a b o) -> s -> Bazaar a b t
(f >==> g) x = f x >>>= g
 

As an aside, Bazaar is also an (Atkey) indexed comonad, and the one that characterizes traversals, similar to how indexed store characterizes lenses. A Lens s t a b is equivalent to a coalgebra s -> Store a b t. A traversal is a similar Bazaar coalgebra:

 
  s -> Bazaar a b t
    ~
  s -> forall f. Applicative f => (a -> f b) -> f t
    ~
  forall f. Applicative f => (a -> f b) -> s -> f t
 

It so happens that Kleisli composition of the Atkey indexed monad above (>==>) is traversal composition.

Anyhow, Bazaar also inherits Applicative structure from Free Applicative:

 
instance Functor (Bazaar a b) where
  fmap f (Bazaar e) = Bazaar $ \k -> fmap f (e k)
 
instance Applicative (Bazaar a b) where
  pure x = Bazaar $ \_ -> pure x
  Bazaar ef < *> Bazaar ex = Bazaar $ \k -> ef k < *> ex k
 

This is actually analogous to the Monoid instance for the free monoid; we just delegate to the underlying structure.

The more exciting thing is that we can fold and traverse over the first argument of Bazaar, just like we can with the free monoid:

 
bfoldMap :: Monoid m => (a -> m) -> Bazaar a b t -> m
bfoldMap f (Bazaar e) = getConst $ e (Const . f)
 
newtype Comp g f a = Comp { getComp :: g (f a) } deriving (Functor)
 
instance (Applicative f, Applicative g) => Applicative (Comp g f) where
  pure = Comp . pure . pure
  Comp f < *> Comp x = Comp $ liftA2 (< *>) f x
 
btraverse
  :: (Applicative f) => (a -> f a') -> Bazaar a b t -> Bazaar a' b t
btraverse f (Bazaar e) = getComp $ e (c . fmap ipure . f)
 

This is again analogous to the free monoid code. Comp is the analogue of Ap, and we use ipure in traverse. I mentioned that Bazaar is a comonad:

 
extract :: Bazaar b b t -> t
extract (Bazaar e) = runIdentity $ e Identity
 

And now we are finally prepared to not cheat:

 
honestTraverse
  :: (Applicative f, Traversable t) => (a -> f b) -> t a -> f (t b)
honestTraverse f = fmap extract . btraverse f . howBizarre
 

So, we can traverse by first turning out Traversable into some structure that's kind of like the free monoid, except having to do with Applicative, traverse that, and then pull a result back out. Bazaar retains the information that we're eventually building back the same type of structure, so we don't need any cheating.

To pull this back around to domains, there's nothing about this code to object to if done in a total language. But, if we think about our free Applicative-ish structure, in Haskell, it will naturally allow infinitary expressions composed of the Applicative operations, just like the free monoid will allow infinitary monoid expressions. And this is okay, because some Applicatives can make sense of those, so throwing them away would make the type not free, in the same way that even finite lists are not the free monoid in Haskell. And this, I think, is compelling enough to say that infinite traversals are right for Haskell, just as they are wrong for Agda.

For those who wish to see executable code for all this, I've put a files here and here. The latter also contains some extra goodies at the end that I may talk about in further installments.

[1] Truth be told, I'm not exactly sure.

[2] It turns out, you can generalize Bazaar to have a correspondence for every choice of p

 
newtype Bizarre p a b t =
  Bizarre { bizarre :: forall f. p f => (a -> f b) -> f t }
 

hence and forth above go through with the more general types. This can be seen here.

It is often stated that Foldable is effectively the toList class. However, this turns out to be wrong. The real fundamental member of Foldable is foldMap (which should look suspiciously like traverse, incidentally). To understand exactly why this is, it helps to understand another surprising fact: lists are not free monoids in Haskell.

This latter fact can be seen relatively easily by considering another list-like type:

 
data SL a = Empty | SL a :> a
 
instance Monoid (SL a) where
  mempty = Empty
  mappend ys Empty = ys
  mappend ys (xs :> x) = (mappend ys xs) :> x
 
single :: a -> SL a
single x = Empty :> x
 

So, we have a type SL a of snoc lists, which are a monoid, and a function that embeds a into SL a. If (ordinary) lists were the free monoid, there would be a unique monoid homomorphism from lists to snoc lists. Such a homomorphism (call it h) would have the following properties:

 
h [] = Empty
h (xs <> ys) = h xs <> h ys
h [x] = single x
 

And in fact, this (together with some general facts about Haskell functions) should be enough to define h for our purposes (or any purposes, really). So, let's consider its behavior on two values:

 
h [1] = single 1
 
h [1,1..] = h ([1] <> [1,1..]) -- [1,1..] is an infinite list of 1s
          = h [1] <> h [1,1..]
 

This second equation can tell us what the value of h is at this infinite value, since we can consider it the definition of a possibly infinite value:

 
x = h [1] <> x = fix (single 1 <>)
h [1,1..] = x
 

(single 1 <>) is a strict function, so the fixed point theorem tells us that x = ⊥.

This is a problem, though. Considering some additional equations:

 
[1,1..] <> [n] = [1,1..] -- true for all n
h [1,1..] = ⊥
h ([1,1..] <> [1]) = h [1,1..] <> h [1]
                   = ⊥ <> single 1
                   = ⊥ :> 1
                   ≠ ⊥
 

So, our requirements for h are contradictory, and no such homomorphism can exist.

The issue is that Haskell types are domains. They contain these extra partially defined values and infinite values. The monoid structure on (cons) lists has infinite lists absorbing all right-hand sides, while the snoc lists are just the opposite.

This also means that finite lists (or any method of implementing finite sequences) are not free monoids in Haskell. They, as domains, still contain the additional bottom element, and it absorbs all other elements, which is incorrect behavior for the free monoid:

 
pure x <> ⊥ = ⊥
h ⊥ = ⊥
h (pure x <> ⊥) = [x] <> h ⊥
                = [x] ++ ⊥
                = x:⊥
                ≠ ⊥
 

So, what is the free monoid? In a sense, it can't be written down at all in Haskell, because we cannot enforce value-level equations, and because we don't have quotients. But, if conventions are good enough, there is a way. First, suppose we have a free monoid type FM a. Then for any other monoid m and embedding a -> m, there must be a monoid homomorphism from FM a to m. We can model this as a Haskell type:

 
forall a m. Monoid m => (a -> m) -> FM a -> m
 

Where we consider the Monoid m constraint to be enforcing that m actually has valid monoid structure. Now, a trick is to recognize that this sort of universal property can be used to define types in Haskell (or, GHC at least), due to polymorphic types being first class; we just rearrange the arguments and quantifiers, and take FM a to be the polymorphic type:

 
newtype FM a = FM { unFM :: forall m. Monoid m => (a -> m) -> m }
 

Types defined like this are automatically universal in the right sense. [1] The only thing we have to check is that FM a is actually a monoid over a. But that turns out to be easily witnessed:

 
embed :: a -> FM a
embed x = FM $ \k -> k x
 
instance Monoid (FM a) where
  mempty = FM $ \_ -> mempty
  mappend (FM e1) (FM e2) = FM $ \k -> e1 k <> e2 k
 

Demonstrating that the above is a proper monoid delegates to instances of Monoid being proper monoids. So as long as we trust that convention, we have a free monoid.

However, one might wonder what a free monoid would look like as something closer to a traditional data type. To construct that, first ignore the required equations, and consider only the generators; we get:

 
data FMG a = None | Single a | FMG a :<> FMG a
 

Now, the proper FM a is the quotient of this by the equations:

 
None :<> x = x = x :<> None
x :<> (y :<> z) = (x :<> y) :<> z
 

One way of mimicking this in Haskell is to hide the implementation in a module, and only allow elimination into Monoids (again, using the convention that Monoid ensures actual monoid structure) using the function:

 
unFMG :: forall a m. Monoid m => FMG a -> (a -> m) -> m
unFMG None _ = mempty
unFMG (Single x) k = k x
unFMG (x :<> y) k = unFMG x k <> unFMG y k
 

This is actually how quotients can be thought of in richer languages; the quotient does not eliminate any of the generated structure internally, it just restricts the way in which the values can be consumed. Those richer languages just allow us to prove equations, and enforce properties by proof obligations, rather than conventions and structure hiding. Also, one should note that the above should look pretty similar to our encoding of FM a using universal quantification earlier.

Now, one might look at the above and have some objections. For one, we'd normally think that the quotient of the above type is just [a]. Second, it seems like the type is revealing something about the associativity of the operations, because defining recursive values via left nesting is different from right nesting, and this difference is observable by extracting into different monoids. But aren't monoids supposed to remove associativity as a concern? For instance:

 
ones1 = embed 1 <> ones1
ones2 = ones2 <> embed 1
 

Shouldn't we be able to prove these are the same, becuase of an argument like:

 
ones1 = embed 1 <> (embed 1 <> ...)
      ... reassociate ...
      = (... <> embed 1) <> embed 1
      = ones2
 

The answer is that the equation we have only specifies the behavior of associating three values:

 
x <> (y <> z) = (x <> y) <> z
 

And while this is sufficient to nail down the behavior of finite values, and finitary reassociating, it does not tell us that infinitary reassociating yields the same value back. And the "... reassociate ..." step in the argument above was decidedly infinitary. And while the rules tell us that we can peel any finite number of copies of embed 1 to the front of ones1 or the end of ones2, it does not tell us that ones1 = ones2. And in fact it is vital for FM a to have distinct values for these two things; it is what makes it the free monoid when we're dealing with domains of lazy values.

Finally, we can come back to Foldable. If we look at foldMap:

 
foldMap :: (Foldable f, Monoid m) => (a -> m) -> f a -> m
 

we can rearrange things a bit, and get the type:

 
Foldable f => f a -> (forall m. Monoid m => (a -> m) -> m)
 

And thus, the most fundamental operation of Foldable is not toList, but toFreeMonoid, and lists are not free monoids in Haskell.

[1]: What we are doing here is noting that (co)limits are objects that internalize natural transformations, but the natural transformations expressible by quantification in GHC are already automatically internalized using quantifiers. However, one has to be careful that the quantifiers are actually enforcing the relevant naturality conditions. In many simple cases they are.

A couple of weeks back one of my coworkers brought to my attention a several hour long workshop in Japan to go over and describe a number of my libraries, hosted by TANAKA Hideyuki — not the voice actor, I checked!

I was incredibly honored and I figured that if that many people (they had 30 or so registered attendees and 10 presentations) were going to spend that much time going over software that I had written, I should at least offer to show up!

I'd like to apologize for any errors in the romanization of people's names or misunderstandings I may have in the following text. My grasp of Japanese is very poor! Please feel free to send me corrections or additions!

Surprise!

Sadly, my boss's immediate reaction to hearing that there was a workshop in Japan about my work was to quip that "You're saying you're huge in Japan?" With him conspicuously not offering to fly me out here, I had to settle for surprising the organizers and attending via Google Hangout.

Commentary and Logs

@nushio was very helpful in getting me connected, and while the speakers gave their talks I sat on the irc.freenode.net #haskell-lens channel and Google Hangout and answered questions and provided a running commentary with more details and references. Per freenode policy the fact that we were logging the channel was announced -- well, at least before things got too far underway.

Here is the IRC session log as a gist. IKEGAMI Daisuke @ikegami__ (ikeg in the IRC log) tried to keep up a high-level running commentary about what was happening in the video to the log, which may be helpful if you are trying to follow along through each retroactively.

Other background chatter and material is strewn across twitter under the #ekmett_conf hash tag and on a japanese twitter aggregator named togetter

(more...)

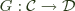Recently, a fellow in category land discovered a fact that we in Haskell land have actually known for a while (in addition to things most of us probably don't). Specifically, given two categories and , a functor , and provided some conditions in hold, there exists a monad , the codensity monad of .

In category theory, the codensity monad is given by the rather frightening expression:

(more...)

Andrej Bauer recently gave a really nice talk on how you can exploit side-effects to make a faster version of Martin Escardo's pseudo-paradoxical combinators.

A video of his talk is available over on his blog, and his presentation is remarkably clear, and would serve as a good preamble to the code I'm going to present below.

Andrej gave a related invited talk back at MSFP 2008 in Iceland, and afterwards over lunch I cornered him (with Dan Piponi) and explained how you could use parametricity to close over the side-effects of monads (or arrows, etc) but I think that trick was lost in the chaos of the weekend, so I've chosen to resurrect it here, and improve it to handle some of his more recent performance enhancements, and show that you don't need side-effects to speed up the search after all!

(more...)

Today I hope to start a new series of posts exploring constructive abstract algebra in Haskell.

In particular, I want to talk about a novel encoding of linear functionals, polynomials and linear maps in Haskell, but first we're going to have to build up some common terminology.

Having obtained the blessing of Wolfgang Jeltsch, I replaced the algebra package on hackage with something... bigger, although still very much a work in progress.

(more...)

Today I'll show that you can derive a Monad from any old Comonad you have lying around.

(more...)

Last time, I started exploring whether or not Codensity was necessary to improve the asymptotic performance of free monads.

This time I'll show that the answer is no; we can get by with something smaller.

(more...)

I've uploaded a package named rad to Hackage for handling reverse-mode automatic differentiation in Haskell.
(more...)

Two concepts come up when talking about information retrieval in most standard documentation, Precision and Recall. Precision is a measure that tells you if your result set contains only results that are relevant to the query, and recall tells you if your result set contains everything that is relevant to the query.

The formula for classical precision is:

However, I would argue that the classical notion of Precision is flawed, in that it doesn't model anything we tend to care about. Rarely are we interested in binary classification, instead we want a ranked classification of relevance.

(more...)

I was asked to give two talks at the Boston Area Haskell User Group for this past Tuesday. The first was pitched at a more introductory level and the second was to go deeper into what I have been using monoids for lately.

The first talk covers an introduction to the mathematical notion of a monoid, introduces some of the features of my Haskell monoids library on hackage, and starts to motivate the use of monoidal parallel/incremental parsing, and the modification use of compression algorithms to recycle monoidal results.

The second talk covers a way to generate a locally-context sensitive parallel/incremental parser by modifying Iteratees to enable them to drive a Parsec 3 lexer, and then wrapping that in a monoid based on error productions in the grammar before recycling these techniques at a higher level to deal with parsing seemingly stateful structures, such as Haskell layout.

1. Introduction To Monoids (PDF)
2. Iteratees, Parsec and Monoids: A Parsing Trifecta (PDF)

Due to a late start, I was unable to give the second talk. However, I did give a quick run through to a few die-hards who stayed late and came to the Cambridge Brewing Company afterwards. As I promised some people that I would post the slides after the talk, here they are.

The current plan is to possibly give the second talk in full at either the September or October Boston Haskell User Group sessions, depending on scheduling and availability.

[ Iteratee.hs ]

Some people have requested my slides from the short talk I gave about monoids and monoidal parsing at Hac Phi. So, here they are.

• Hac Phi Slides (Powerpoint 2007)
• Hac Phi Slides (PDF)

There will be more to come at the next Boston Haskell User Group in August, where it looks like I'll be giving two short talks covering monoids. I may use the monoidal parsing engine from Kata as an example for the advanced talk if I have time and will start to cover parsing larger classes of grammars in general (regular languages, CFGs/TIGs, TAGs, PEGs, LALR, attribute-grammars, etc.)

About a year back I posted a field guide of recursion schemes on this blog and then lost it a few months later when I lost a couple of months of blog entries to a crash. I recently recovered the table of recursion schemes from the original post thanks to Google Reader's long memory and the help of Jeff Cutsinger.

The following recursion schemes can be found in category-extras, along with variations on the underlying themes, so this should work as a punch-list.

* This gives rise to a family of related recursion schemes, modeled in category-extras with distributive law combinators
† The scheme can be generalized to accept one or more F-distributive (co)monads.

Grant B. asked me to post the derivation for the right and left Kan extension formula used in previous Kan Extension posts (1,2). For that we can turn to the definition of Kan extensions in terms of ends, but first we need to take a couple of steps back to find a way to represent (co)ends in Haskell.

(more...)

I think I may spend a post or two talking about Kan extensions.

They appear to be black magic to Haskell programmers, but as Saunders Mac Lane said in Categories for the Working Mathematician:

All concepts are Kan extensions.

So what is a Kan extension? They come in two forms: right- and left- Kan extensions.

First I'll talk about right Kan extensions, since Haskell programmers have a better intuition for them.

(more...)

 
> import Control.Arrow ((|||),(&&&),left)
> newtype Mu f = InF { outF :: f (Mu f) }
 

I want to talk about a novel recursion scheme that hasn't received a lot of attention from the Haskell community and its even more obscure dual -- which is necessarily more obscure because I believe this is the first time anyone has talked about it.

Jiri Adámek, Stefan Milius and Jiri Velebil have done a lot of work on Elgot algebras. Here I'd like to translate them into Haskell, dualize them, observe that the dual can encode primitive recursion, and provide some observations.

You can kind of think an Elgot algebra as a hylomorphism that cheats.

 
> elgot :: Functor f => (f b -> b) -> (a -> Either b (f a)) -> a -> b
> elgot phi psi = h where h = (id ||| phi . fmap h) . psi
 

(more...)

Ok, I decided to take a step back from my flawed approach in the last post and play with the idea of power series of functors from a different perspective.

I dusted off my copy of Herbert Wilf's generatingfunctionology and switched goals to try to see some well known recursive functors or species as formal power series. It appears that we can pick a few things out about the generating functions of polynomial functors.

As an example:

 
Maybe x = 1 + x
 

Ok. We're done. Thank you very much. I'll be here all week. Try the veal...

For a more serious example, the formal power series for the list [x] is just a geometric series:

(more...)

The post below will only compile on a version of GHC >= 6.9, since it uses type families.

(more...)