Kan Extensions III: As Ends and Coends

Grant B. asked me to post the derivation for the right and left Kan extension formula used in previous Kan Extension posts (1,2). For that we can turn to the definition of Kan extensions in terms of ends, but first we need to take a couple of steps back to find a way to represent (co)ends in Haskell.

Dinatural Transformations

Rather than repeat the definition here, we'll just note we can define a dinatural transformation in Haskell letting polymorphism represent the family of morphisms.

type Dinatural f g = forall a. f a a -> g a a

Ends

So what is an end?

An end is a universal dinatural transformation from some object e to some functor s.

Diving into the formal definition:

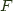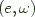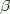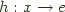Given a functor $F : \mathcal{C}^{op} \times \mathcal{C} \to \mathcal{D}$, and end of $F$ is a pair $(e,\omega)$ where $e$ is an object of $\mathcal{D}$ and omega is a dinatural transformation from e to S such that given any other dinatural transformation $\beta$ to S from another object x in $\mathcal{D}$, there exists a unique morphism $h : x \to e$, such that 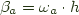$\beta_a = \omega_a \cdot h$ for every $a$ in $\mathcal{C}$.

We usually choose to write ends as $e = \int_c S(c,c)$, and abuse terminology calling $e$ the end of $S$.

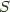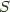Note this uses a dinatural transformation from an object $x$ in $\mathcal{D}$, which we can choose to represent an arbitrary dinatural transformation from an object $x$ to a functor $S$ in terms of a dinatural transformation from the constant bifunctor:

newtype Const x a b = Const { runConst :: x }

This leaves us with the definition of a dinatural transformation from an object as:

Dinatural (Const x) s ~ forall a. Const x a a -> s a a

but the universal quantification over the Const term is rather useless and the Const bifunctor is supplying no information so we can just specialize that down to:

type DinaturalFromObject x s = x -> forall a. s a a

Now, clearly for any such transformation, we could rewrite it trivially using the definition:

type End s = forall a. s a a

with 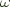$\omega$ = id.

type DinaturalFromObject x s = x -> End s

And so End above fully complies with the definition for an end, and we just say e = End s abusing the terminology as earlier. The function 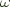$\omega$ = id is implicit.

For End to be a proper end, we assume that s is contravariant in its first argument and covariant in its second argument.

Example: Hom

A good example of this is (->) in Haskell, which is as category theory types would call it the Hom functor for Hask. Then End (->) = forall a. a -> a which has just one inhabitant id if you discard cheating inhabitants involving fix or undefined.

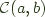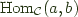We write $\mathcal{C}(a,b)$ or $\mathrm{Hom}_\mathcal{C}(a,b)$ to denote a -> b. Similarly we use 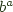$b^a$ to denote an exponential object within a category, and since in Haskell we have first class functions using the same syntax this also translates to a -> b. We'll need these later.

Example: Natural Transformations

If we define:

newtype HomFG f g a b =
  HomFG { runHomFG :: f a -> g b }

then we could of course choose to define natural transformations in terms of End as:

type Nat f g = End (HomFG f g) -- forall a. f a -> g a

Right Kan Extension as an End

Turning to Wikipedia or Categories for the Working Mathematician you can find the following definition for right Kan extension of 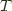$T$ along $K$ in terms of ends.

$(\mathrm{Ran}_KT)c=\int_m Tm^{\mathbf{C}(c,Km)}$

Working by rote, we note that 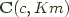$\mathbf{C}(c,Km)$ is just c -> K m as noted above, and that 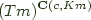$(Tm)^{\mathbf{C}(c,Km)}$ is then just (c -> K m) -> T m'. So now we just have to take the end over that, and read off:

newtype RanT k t c m m' = (c -> k m) -> t m'
type Ran k t c = End (RanT k t c)

Which, modulo newtype noise is the same as the type previously supplied type:

newtype Ran f g c = Ran { runRan :: forall m. (c -> f m) -> g m }

Coends

The derivation for the left Kan extension follows similarly from defining coends over Hask in terms of existential quantification and copowers as products.

The coend derivation is complicated slightly by Haskell's semantics. Disposing of the constant bifunctor as before we get:

type DinaturalToObject s c = forall a. (s a a -> c)

Which since we want to be able to box up the s a a term separately, we need to use existential quantification.

(forall a. s a a -> c) ~ (exists a. s a a) -> c

We cannot represent this directly in terms of a type annotation in Haskell, but we can do so with a data type:

data Coend f = forall a. Coend (f a a)

Recall that in Haskell, existential quantification is represented by using universal quantification outside of the type constructor.

The main difference is that in our coend 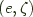$(e,\zeta)$ the function $\zeta$ is now runCoend instead of id, because we have a Coend data constructor around the existential. Technicalities make it a little more complicated than that even, because you can't define a well-typed runCoend and have to use pattern matching on the Coend data constructor to avoid having an existentially quantified type escape the current scope, but the idea is the same.

Left Kan Extension as a Coend

Then given the definition for the left Kan extension of 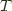$T$ along $K$ as a coend:

$(\mathrm{Lan}_KT)c=\int^m \mathbf{C}(Km,c)\cdot Tm$

we can read off:

data LanT k t c m m' = LanT (k m -> c) (t m')
type Lan k t c = Coend (LanT k t c)

Which is almost isomorphic to the previously supplied type:

data Lan k t c = forall m. Lan (k m -> c) (t m)

except for the fact that we had to use two layers of data declarations when using the separate Coend data type, so we introduced an extra place for a $\perp$ to hide.

A newtype isn't allowed to use existential quantification in Haskell, so this form forces a spurious case analysis that we'd prefer to do without. This motivates why category-extras uses a separate definition for Lan rather than the more elaborate definition in terms of Coend.

[Edit: Fixed a typo in the definition of RanT]