Fri 21 Oct 2022
Internalized Guarded Recursion for Equational Reasoning
Posted by Gershom Bazerman under Data Structures , HaskellComments Off
I recently presented a paper on infinite traversals at the Haskell Symposium: A totally predictable outcome: an investigation of traversals of infinite structures. The main result there is a characterization of when a call to traverse on an infinite Traversable functor (like an infinite lazy list) yields a non-bottom result. It turns out this is a condition on the Applicative one traverses with that loosely amounts to it having only a single data constructor. What I want to talk about here is how the technique introduced in that paper, which I call "internal guarded recursion" can be used not only in a lightweight formal way to prove characterization theorems or the like, but just in everyday programming as a "back of the envelope" or "streetfighting" hack to quickly figure out when recursive functional programs terminate and when they go into infinite loops.
Let's talk about the basic trick that makes the whole thing work. First, we introduce an abstract newtype for identity, which we will disallow pattern matching against, and instead only allow access to through the structure of an applicative functor.
newtype Later a = Later a deriving Functor instance Applicative Later where pure = Later Later f < *> Later x = Later (f x)
Next, we introduce the only function allowed to perform recursion:
lfix :: (Later a -> a) -> a lfix f = fix (f . pure)
This function has almost the same type signature as the typical fixpoint operator, but it "guards" the argument to the function it is taking the fixedpoint of by our abstract Later type constructor.
Now, if you write code that only has recursion via `lfix` and no other function can implicitly or explicitly invoke itself (which the paper refers to as "working in the guarded fragment), your code will never produce a bottom. You can have whatever sorts of recursive Haskell '98 data definitions you like, it doesn't matter! (However, if you have "impredicative" datatypes that pack polymorphic functions into them, I think it would matter... but let's leave that aside). Try, for example, using only this form of recursion, to write a function that produces an infinite list. You'll realize that each recursive step requires using up one Later constructor as "fuel". And since there's no way to get an infinite amount of Later constructors to begin with, you'll only be able to produce lists of finite depth.
However, we can create related data structures to our existing ones, which "guard" their own recurrence behind a Later type constructor as well -- and we can create, consume and manipulate those also, and also do so without risk of writing an expression that produces a bottom. For example, here is the type of possibly infinite lists:
data Stream a = Nil | Cons a (Later (Stream a)
And here is a function that interleaves two such lists:
sinterleave :: Stream a -> Stream a -> Stream a sinterleave = lfix $ \f s1 s2 -> case s1 of (Cons x xs) -> Cons x (f < *> pure s2 < *> xs) _ -> s2
Now, I'm going to diverge from the paper and pose a sort of general problem, based on some discussions I had at ICFP. Suppose you have some tricky recursion, possibly involving "tying the knot" and want to show that it terminates, or to figure out under which conditions it terminates -- how can you do that? It turns out that internal guarded recursion can help! Here's the recipe:
1. Write your function using only explicit recursion (via fix).
2. Change fix to lfix
3. Figure out what work you have to do adding applicative operations involving Later to fix the types.
The paper has in it a general theorem that says, loosely speaking, that if you have code involving lfix and Later, and change that back to fix and erase all the mucking around with Later you get "essentially the same" function, and you still have a guarantee it won't produce bottoms. So this just turns that around -- start with your normal code, and show you can write it even in the guarded fragment, and then that tells you the properties of your original code!
I'll present this approach to reasoning about two tricky but well known problems in functional programming. First, as suggested by Tom Schrijvers as a question at the talk, is the famous "repmin" function introduced by Bird in 1984. This is a program that makes essential use of laziness to traverse a tree only once, but replacing each element in the tree by the minimum element anywhere in the tree. Here's a quick one-liner version, making use of traversal in the writer monad -- it works over any finite traversable structure, including typical trees. But it is perhaps easiest to test it over lists. For now, we'll ignore the issue of what happens with traversals of infinite structures, as that will complicate the example.
repMin1 :: (Traversable t, Ord a) => t a -> t a repMin1 xs = let (ans,m) = fmap minimum . runWriter $ traverse (\x -> tell [x] >> pure m) xs in ans
Note that this above definition makes use of a recursive definition -- the body of the definition of (ans,m) makes use of the m being defined. This works because the definition does not pattern match on the m to compute -- otherwise we would bottom out. Using internal guarded recursion, we can let the type system guide us into rewriting our code into a form where it is directly evident that this does not bottom, rather than relying on careful reasoning about semantics. The first step is to mechanically transform the initial definition into one that is exactly the same, but where the implicit recursion has been rendered explicit by use of fix:
repMin2 :: (Traversable t, Ord a) => t a -> t a repMin2 xs = let res = fix go in fst res where go res = fmap minimum . runWriter $ traverse (\x -> tell [x] >> pure (snd res)) xs
The next step is to now replace fix by lfix. When we do so, the type of go will no longer be correct. In particular, its argument, res will now be guarded by a Later. So we can no longer apply snd directly to it, but instead have to fmap. The compiler will notice this and yell at us, at which point we make that small tweak as well. In turn, this forces a change to the type signature of the overall function. With that done, everything still checks!
repMin3 :: (Traversable t, Ord a) => t a -> t (Later a) repMin3 xs = let res = lfix go in fst res where go res = fmap minimum . runWriter $ traverse (\x -> tell [x] >> pure (snd < $> res)) xs
We have now verified that the original repMin1 function does not bottom out on finite structures. Further, the "one layer" of Later in the type of repMin3 tells us that there was exactly one recursive step invoked in computing the final result!
The astute reader may have noticed a further complication -- to genuinely be in the guarded recursive fragment, we need to make sure all functions in sight have not been written using standard recursion, but only with guarded recursion. But in fact, both minimum and traverse are going to be written recursively! We limited ourselves to considering finite trees to avoid worrying about this for our example. But let's now briefly consider what happens otherwise. By the results in the paper, we can still use a guarded recursive traverse in the writer monad, which will produce a potentially productive stream of results -- one where there may be arbitrarily many Later steps between each result. Further, a guarded recursive minimum on such a stream, or even on a necessarily productive Stream as given above, will necessarily produce a value that is potentially infinitely delayed. So without grinding out the detailed equational substitution, we can conclude that the type signature we would have to produce in the case of a potentially infinite tree would in fact be: (Traversable t, Ord a) => t a -> t (Partial a) -- where a partial value is one that may be delayed behind an arbitrary (including infinite) sequence of Later. This in turns tells us that repMin on a potentially infinite structure would still produce safely the skeleton of the structure we started with. However, at each individual leaf, the value would potentially be bottom. And, in fact, by standard reasoning (it takes an infinite amount of time to find the minimum of an infinite stream), we can conclude that when repMin is run on an infinite structure, then indeed each leaf would be bottom!
We'll now consider one further example, arising from work by Kenneth Foner on fixed points of comonads. In their paper, Foner provides an efficient fixed point operator for comonads with an "apply" operator, but also makes reference to an inefficient version which they believe has the same semantics, and was introduced by Dominic Orchard. This latter operator is extremely simple to define, and so an easy candidate for an example. We'll first recall the methods of comonads, and then introduce Orchard's fixed-point:
class Functor w => Comonad w where extract :: w a -> a duplicate :: w a -> w (w a) extend :: (w a -> b) -> w a -> w b cfix f :: Comonad w => (w a -> a) -> w a cfix f = fix (extend f)
So the question is -- when does cfix not bottom out? To answer this, we again just change fix to lfix and let the typechecker tells us what goes wrong. We quickly discover that our code no longer typechecks, because lfix enforces we are given a Later (w a) but the argument to extend f needs to be a plain old w a. We ask ghc for the type of the intermediate conversion function necessary, and arrive at the following:
lcfix :: Comonad w => (Later (w b) -> w a) -> (w a -> b) -> w b lcfix conv f = lfix (extend f . conv)
So we discover that comonad fix will not bottom when we can provide some conv function that is "like the identity" (so it erases away when we strip out the mucking about with Later) but can send Later (w a) -> w b. If we choose to unify a and b, then this property (of some type to be equipped with an "almost identity" between it and it delayed by a Later) is examined in the paper at some length under the name "stability" -- and our conclusion is that cfix will terminate when the type w a is stable (which is to say that it in one way or another represents a potentially partial value). Also from the paper, we know that one easy way to get stability is when the type w is Predictable -- i.e. when it has an "almost identity" map Later (w a) -> w (Later a) and when a itself is stable. This handles most uses of comonad fix -- since functors of "fixed shape" (otherwise known as representable, or iso to r -> a for a fixed r) are all stable. And the stability condition on the underlying a tells us that even though we'll get out a perfectly good spine, whether or not there will be a bottom value at any given location in the resultant w a depends on the precise function being passed in.
In fact, if we simply start with the idea of predictability in hand, we can specialize the above code in a different way, by taking predict itself to be our conversion function, and unifying b with Later a, which yields the following:
lcfix2 :: (Comonad w, Predict w) => (w (Later a) -> a) -> w a lcfix2 f = lfix (extend f . predict)
This signature is nice because it does not require stability -- i.e. there is no possibility of partial results. Further, it is particularly suggestive -- it looks almost like that of lfix but lifts both the input to the argument and the output of the fixed-point up under a w. This warns us how hard it is to get useful values out of fixing a comonad -- in particular, just as with our lfix itself, we can't directly pattern match on the values we are taking fixed points of, but instead only use them in constructing larger structures.
These examples illustrate both the power of the internal guarded recursion approach, and also some of its limits. It can tell us a lot of high level information about what does and doesn't produce bottoms, and it can produce conditions under which bottoms will never occur. However, there are also cases where we have code that sometimes bottoms, depending on specific functions it is passed -- the fact that it potentially bottoms is represented in the type, but the exact conditions under which bottoms will or will not occur aren't able to be directly "read off". In fact, in the references to the paper, there are much richer variants of guarded recursion that allow more precision in typing various sorts of recursive functions, and of course there is are general metamathematical barriers to going sufficiently far -- a typing system rich enough to say if any integer function terminates is also rich enough to say if e.g. the collatz conjecture is true or not! But with all those caveats in mind, I think this is still a useful tool that doesn't only have theoretical properties, but also practical use. The next time you have a tricky recursive function that you're pretty sure terminates, try these simple steps: 1) rewrite to use explicit fixed points; 2) change those to guarded recursive fixed points; 3) let ghc guide you in fixing the types; 4) see what you learn!

 and
and  , a functor
, a functor 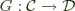 , and provided some conditions in
, and provided some conditions in  , the codensity monad of
, the codensity monad of  .
.![$ T^G(a) = \int_r \left[\mathcal{D}(a, Gr), Gr\right] $ $ T^G(a) = \int_r \left[\mathcal{D}(a, Gr), Gr\right] $](http://comonad.com/latex/050bb5034bed82159df4c52c89c07f3c.png)