The Comonad.Reader

Back in 2011, in an influential blog post [1], Robert Harper coined the term "computational trinitarianism" to describe an idea that had been around a long time — that the connection between programming languages, logic, and categories, most famously expressed in the Curry-Howard-Lambek correspondence — should guide the practice of researchers into computation. In particular "any concept arising in one aspect should have meaning from the perspective of the other two". This was especially satisfying to those of us trying learning categorical semantics and often finding it disappointing how little it is appreciated in the computer science community writ large.

1. Categories

Over the years I've thought about trinitarianism a lot, and learned from where it fails to work as much as where it succeeds. One difficulty is that learning to read a logic like a type theory, or vice versa, is almost a definitional trick, because it occurs at the level of reinterpretation of syntax. With categories it is typically not so easy. (There is a straightforward version of categorical semantics like this — yielding "syntactic categories" — but it is difficult to connect it to the broader world of categorical semantics, and often it is sidestepped in favor of deeper models.)

One thing I came to realize is that there is no one notion of categorical semantics — the way in which the simply typed lambda calculus takes models in cartesian closed categories is fundamentally unlike the way in which linear logics take models in symmetric monoidal categories. If you want to study models of dependent type theories, you have a range of approaches, only some of which have been partially unified by Ahrens, Lumsdaine and Voevodsky in particular [2]. And then there are the LCCC models pioneered by Seely for extensional type theory, not to mention the approach that takes semantics directly in toposes, or in triposes (the latter having been invented to unify a variety of structures, and in the process giving rise to still more questions). And then there is the approach that doesn't use categories at all, but multicategories.

Going the other way, we also run into obstacles: there is a general notion, opposite to the "syntactic category" of a type theory, which is the "internal logic" of a category. But depending on the form of category, "internal logic" can take many forms. If you are in a topos, there is a straightforward internal logic called the Mitchell–Bénabou language. In this setting, most "logical" operations factor through the truth-lattice of the subobject classifier. This is very convenient, but if you don't have a proper subobject classifier, then you are forced to reach for other interpretations. As such, it is not infrequently the case that we have a procedure for deriving a category from some logical theory, and a procedure for constructing a logical theory from some category, but there is no particular reason to expect that where we arrive, when we take the round-trip, is close to, much less precisely, where we began.

2. Spaces, Logics

Over the past few years I've been in a topos theory reading group. In the course of this, I've realized at least one problem with all the above (by no means the only one) — Harper's holy trinity is fundamentally incomplete. There is another structure of interest — of equal weight to categories, logics, and languages — which it is necessary to understand to see how everything fits. This structure is spaces. I had thought that it was a unique innovation of homotopy type theory to consider logics (resp. type theories) that took semantics in spaces. But it turns out that I just didn't know the history of constructive logic very well. In fact, in roughly the same period that Curry was exploring the relationship of combinatory algebras to logic, Alfred Tarski and Marshall Stone were developing topological models for intuitionistic logic, in terms of what we call Heyting Algebras [3] [4]. And just as, as Harper explained, logic, programming and category theory give us insights into implication in the form of entailment, typing judgments, and morphisms, so to, as we will see, do spaces.

A Heyting algebra is a special type of distributive lattice (partially ordered set, equipped with meet and join operations, such that meet and join distribute over one another) which has an implication operation that satisfies curry/uncurry adjointness — i.e. such that c ∧ a ≤ b < -> c ≤ a → b. (Replace meet here by "and" (spelled "*"), and ≤ by ⊢ and we have the familiar type-theoretic statement that c * a ⊢ b < -> c ⊢ a → b).

If you haven't encountered this before, it is worth unpacking. Given a set, we equip it with a partial order by specifying a "≤" operation, such that a ≤ a, if a ≤ b and b ≤ a, then a = b, and finally that if a ≤ b and b ≤ c, then a ≤ c. We can think of such things as Hasse diagrams — a bunch of nodes with some lines between them that only go upwards. If a node b is reachable from a node a by following these upwards lines, then a ≤ b. This "only upwards" condition is enough to enforce all three conditions. We can define ∨ (join) as a binary operation that takes two nodes, and gives a node a ∨ b that is greater than either node, and furthermore is the uniquely least node greater than both of them. (Note: A general partial order may have many pairs of nodes that do not have any node greater than both of them, or may that may have more than one incomparable node greater than them.) We can define ∧ (meet) dually, as the uniquely greatest node less than both of them. If all elements of a partially ordered set have a join and meet, we have a lattice.

It is tempting to read meet and join as "and" and "or" in logic. But these logical connectives satisfy an additional important property — distributivity: a & (b | c) = (a & b) | (a & c). (By the lattice laws, the dual property with and swapped with or is also implied). Translated for lattices this reads: a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c). Rather than thinking just about boolean logic, we can think about lattices built from sets — with meets as union, join as intersection, and ≤ given by inclusion. It is easy to verify that such lattices are distributive. Furthermore, every distributive lattice can be given (up to isomorphism) as one built out of sets in this way. While a partially ordered set can have a Hasse diagram of pretty arbitrary shape, a lattice is more restrictive — I imagine it as sort of the tiled diamonds of an actual lattice like one might use in a garden, but with some nodes and edges possibly removed.

Furthermore, there's an amazing result that you can tell if a lattice is distributive by looking for just two prototypical non-distributive lattices as sublattices. If neither is contained in the original lattice, then the lattice is distributed. These tell us how distribution can fail in two canonical ways. The first is three incomparable elements, all of which share a common join (the top) and meet (the bottom). The join of anything but their bottom element with them is therefore the top. Hence if we take the meet of two joins, we still get the top. But the meet of any two non-top elements is the bottom and so, if we take the join of any element with the meet of any other two, we get back to the first element, not all the way to the top, and the equality fails. The second taboo lattice is constructed by having two elements in an ordered relationship, and another incomparable to them — again augmented with a bottom and top. A similar argument shows that if you go one way across the desired entity, you pick out the topmost of the two ordered elements, and the other way yields the bottommost. (The wikipedia article on distributive lattices has some very good diagrams to visualize all this). So a distributive lattice has even more structure than before — incomparable elements must have enough meets and joins to prevent these sublattices from appearing, and this forces even more the appearance of a tiled-diamond like structure.

To get us to a Heyting algebra, we need more structure still — we need implication, which is like an internal function arrow, or an internal ≤ relation. Recall that the equation we want to satisfy is "c ∧ a ≤ b < -> c ≤ a → b". The idea is that we should be able to read ≤ itself as an "external implication" and so if c and a taken together imply b, "a implies b" is the portion of that implication if we "only have" c. We can see it as a partial application of the external implication. If we have a lattice that permits infinite joins (or just a finite lattice such that we don't need them), then it is straightforward to see how to construct this. To build a → b, we just look at every possible choice of c that satisfies c ∧ a ≤ b, and then take the join of all of them to be our object a → b. Then, by construction, a → b is necessarily greater than or equal to any c that satisfies the left hand side of the equation. And conversely, any element that a → b is greater than is necessarily one that satisfies the left hand side, and the bi-implication is complete. (This, by the way, gives a good intuition for the definition of an exponential in a category of presheaves). Another way to think of a → b is as the greatest element of the lattice such that a → b ∧ a ≤ b (exercise: relate this to the first definition). It is also a good exercise to explore what happens in certain simple cases — what if a is 0 (false)? What if it is 1? The same as b? Now ask the same questions of b.

So why is a Heyting algebra a topological construct? Consider any topological space as given by a collection of open sets, satisfying the usual principles (including the empty set and the total set, and closed under union and finite intersection). These covers have a partial ordering, given by containment. They have unions and intersections (all joins and meets), a top and bottom element (the total space, and the null space). Furthermore, they have an implication operation as described above. As an open set, a → b is given by the meet of all opens c for which a ∧ c ≤ b. (We can think of this as "the biggest context, for which a ⊢ b"). In fact, the axioms for open sets feel almost exactly like the rules we've described for Heyting algebras. It turns out this is only half true — open sets always give Heyting algebras, and we can turn every Heyting algebra into a space. However, in both directions the round trip may take us to somewhere slightly different than where we started. Nonetheless it turns out that if we take complete Heyting algebras where finite meets distribute over infinite joins, we get something called "frames." And the opposite category of frames yields "locales" — a suitable generalization of topological spaces, first named by John Isbell in 1972 [5]. Spaces that correspond precisely to locales are called sober, and locales that correspond precisely to spaces are said to have "enough points" or be "spatial locales".

In fact, we don't need to fast-forward to 1972 to get some movement in the opposite direction. In 1944, McKinsey and Tarski embarked on a program of "The Algebra of Topology" which sought to describe topological spaces in purely algebraic (axiomatic) terms [6]. The resultant closure algebras (these days often discussed as their duals, interior algebras) provided a semantics for S4 modal logic. [7] A further development in this regard came with Kripke models for logic [8] (though arguably they're really Beth models [9]).

Here's an easy way to think about Kripke models. Start with any partial ordered set. Now, for each object, instead consider instead all morphisms into it. Since each morphism from any object a to any object b exists only if a ≤ b, and we consider such paths unique (if there are two "routes" showing a ≤ b, we consider them the same in this setting) this amounts to replacing each element a with the set of all elements ≤ a. (The linked pdf does this upside down, but it doesn't really matter). Even though the initial setting may not have been Heyting algebra, this transformed setting is a Heyting algebra. (In fact, by a special case of the Yoneda lemma!). This yields Kripke models.

Now consider "collapsings" of elements in the initial partial order — monotone downwards maps taken by sending some elements to other elements less than them in a way that doesn't distort orderings. (I.e. if f(a) ≤ f(b) in the collapsed order, then that means that a ≤ b in the original order). Just as we can lift elements from the initial partial order into their downsets (sets of elements less than them) in the kripkified Heyting Algebra, we can lift our collapsing functions into collapsing functions in our generated Heyting Algebra. With a little work we can see that collapsings in the partial order also yield collapsings in the Heyting Algebra.

Furthermore, it turns out, more or less, that you can generate every closure algebra in this way. Now if we consider closure algebras a bit (and this shouldn't surprise us if we know about S4), we see that we can always take a to Ca, that if we send a → b, then we can send Ca → Cb, and furthermore that CCa → Ca in a natural way (in fact, they're equal!). So closure algebras have the structure of an idempotent monad. (Note: the arrows here should not be seen as representing internal implication — as above they represent the logical turnstile ⊢ or perhaps, if you're really in a Kripke setting, the forcing turnstile ⊩).

Now we have a correspondence between logic and computation (Curry-Howard), logic and categories (Lambek-Scott), and logic and spaces (Tarski-Stone). So maybe, instead of Curry-Howard-Lambek, we should speak of Curry-Howard-Lambek-Scott-Tarski-Stone! (Or, if we want to actually bother to say it, just Curry-Howard-Lambek-Stone. Sorry, Tarski and Scott!) Where do the remaining correspondences arise from? A cubical Kan operation, naturally! But let us try to sketch in a few more details.

3. Spaces, Categories

All this about monads and Yoneda suggests that there's something categorical going on. And indeed, there is. A poset is, in essence, a "decategorified category" — that is to say, a category where any two objects have at most one morphism between them. I think of it as if it were a balloon animal that somebody let all the air out of. We can pick up the end of our poset and blow into it, inflating the structure back up, and allowing multiple morphisms between each object. If we do so, something miraculous occurs — our arbitrary posets turn into arbitrary categories, and the induced Heyting algebra from their opens turns into the induced category of set-valued presheaves of that category. The resultant structure is a presheaf topos. If we "inflate up" an appropriate notion of a closure operator we arrive at a Grothendieck topos! And indeed, the internal language of a topos is higher-order intuitionistic type theory [10].

4. Spaces, Programming Languages

All of this suggests a compelling story: logic describes theories via algebraic syntax. Equipping these theories with various forms of structural operations produces categories of one sort or another, in the form of fibrations. The intuition is that types are spaces, and contexts are also spaces. And furthermore, types are covered by the contexts in which their terms may be derived. This is one sense in which we it seems possible to interpret the Meillies/Zeilberger notion of a type refinement system as a functor [11].

But where do programming languages fit in? Programming languages, difficult as it is to sometimes remember, are more than their type theories. They have a semantic of computation as well. For example, a general topos does not have partial functions, or a fixed point combinator. But computations, often, do. This led to one of the first applications of topology to programming languages — the introduction of domain theory, in which terms are special kinds of spaces — directed complete partial orders — and functions obey a special kind of continuity (preservation of directed suprema) that allows us to take their fixed points. But while the category of dcpos is cartesian closed, the category of dcpos with only appropriately continuous morphisms is not. Trying to resolve this gap, one way or another, seems to have been a theme of research in domain theory throughout the 80s and 90s [12].

Computations can also be concurrent. Topological and topos-theoretic notions again can play an important role. In particular, to consider two execution paths to be "the same" one needs a notion of equivalence. This equivalence can be seen, stepwise, as a topological "two-cell" tracing out at each step an equivalence between the two execution paths. One approach to this is in Joyal, Nielson and Winskel's treatment of open maps [13]. I've also just seen Patrick Schultz and David I. Spivak's "Temporal Type Theory" which seems very promising in this regard [14].

What is the general theme? Computation starts somewhere, and then goes somewhere else. If it stayed in the same place, it would not "compute". A computation is necessarily a path in some sense. Computational settings describe ways to take maps between spaces, under a suitable notion of topology. To describe the spaces themselves, we need a language — that language is a logic, or a type theory. Toposes are a canonical place (though not the only one) where logics and spaces meet (and where, to a degree, we can even distinguish their "logical" and "spatial" content). That leaves categories as the ambient language in which all this interplay can be described and generalized.

5. Spaces, Categories

All the above only sketches the state of affairs up to roughly the mid '90s. The connection to spaces starts in the late 30s, going through logic, and then computation. But the categorical notion of spaces we have is in some sense impoverished. A topos-theoretic generalization of a space still only describes, albeit in generalized terms, open sets and their lattice of subobject relations. Spaces have a whole other structure built on top of that. From their topology we can extract algebraic structures that describe their shape — this is the subject of algebraic topology. In fact, it was in axiomatizing a branch of algebraic topology (homology) that category theory was first compelled to be invented. And the "standard construction" of a monad was first constructed in the study of homology groups (as the Godement resolution).

What happens if we turn the tools of categorical generalization of algebraic topology on categories themselves? This corresponds to another step in the "categorification" process described above. Where to go from "0" to "1" we took a partially ordered set and allowed there to be multiple maps between objects, to go from "1" to "2" we can now take a category, where such multiple maps exist, and allow there to be multiple maps between maps. Now two morphisms, say "f . g" and "h" need not merely be equal or not, but they may be "almost equal" with their equality given by a 2-cell. This is just as two homotopies between spaces may themselves be homotopic. And to go from "2" to "3" we can continue the process again. This yields n-categories. An n-category with all morphisms at every level invertible is an (oo,0)-category, or an infinity groupoid. And in many setups this is the same thing as a topological space (and the question of which setup is appropriate falls under the name "homotopy hypothesis" [15]). When morphisms at the first level (the category level) can have direction (just as in normal categories) then those are (oo,1)-categories, and the correspondence between groupoids and spaces is constructed as an equivalence of such categories. These too have direct topological content, and one setting in which this is especially apparent is that of quasi-categories, which are (oo,1)-categories that are built directly from simplicial sets — an especially nice categorical model of spaces (the simplicial sets at play here are those that satisfy a "weak" Kan condition, which is a way of asking that composition behave correctly).

It is in these generalized (oo,1)-toposes that homotopy type theory takes its models. And, it is hypothesized that a suitable version of HoTT should in fact be the initial model (or "internal logic") of an "elementary infinity topos" when we finally figure out how to describe what such a thing is.

So perhaps it is not that we should be computational trinitarians, or quadrinitarians. Rather, it is that the different aspects which we examine — logic, languages, categories, spaces — only appear as distinct manifestations when viewed at a low dimensionality. In the untruncated view of the world, the modern perspective is, perhaps, topological pantheism — spaces are in all things, and through spaces, all things are made as one.

Thanks to James Deikun and Dan Doel for helpful technical and editorial comments

[1] https://existentialtype.wordpress.com/2011/03/27/the-holy-trinity/
[2] https://arxiv.org/abs/1705.04310
[3] http://www.sciacchitano.it/Tempo/Aussagenkalk%C3%BCl%20Topologie.pdf
[4] https://eudml.org/doc/27235
[5] http://www.mscand.dk/article/view/11409
[6] https://www.dimap.ufrn.br/~jmarcos/papers/AoT-McKinsey_Tarski.pdf
[7] https://logic.berkeley.edu/colloquium/BezhanishviliSlides.pdf
[8] www2.math.uu.se/~palmgren/tillog/heyting3.pdf
[9] http://festschriften.illc.uva.nl/j50/contribs/troelstra/troelstra.pdf
[10] http://www.sciencedirect.com/science/article/pii/0022404980901024
[11] https://arxiv.org/abs/1310.0263
[12] https://www.dpmms.cam.ac.uk/~martin/Research/Oldpapers/synthetic91.pdf
[13] http://www.brics.dk/RS/94/7/index.html
[14] https://arxiv.org/abs/1710.10258
[15] https://ncatlab.org/nlab/show/homotopy+hypothesis

A common occurrence in category theory is the adjoint triple. This is a pair of adjunctions relating three functors:

F ⊣ G ⊣ H
F ⊣ G, G ⊣ H

Perhaps part of the reason they are so common is that (co)limits form one:

colim ⊣ Δ ⊣ lim

where Δ : C -> C^J is the diagonal functor, which takes objects in C to the constant functor returning that object. A version of this shows up in Haskell (with some extensions) and dependent type theories, as:

∃ ⊣ Const ⊣ ∀
Σ ⊣ Const ⊣ Π

where, if we only care about quantifying over a single variable, existential and sigma types can be seen as a left adjoint to a diagonal functor that maps types into constant type families (either over * for the first triple in Haskell, or some other type for the second in a dependently typed language), while universal and pi types can be seen as a right adjoint to the same.

It's not uncommon to see the above information in type theory discussion forums. But, there are a few cute properties and examples of adjoint triples that I haven't really seen come up in such contexts.

To begin, we can compose the two adjunctions involved, since the common functor ensures things match up. By calculating on the hom definition, we can see:

Hom(FGA, B)     Hom(GFA, B)
    ~=              ~=
Hom(GA, GB)     Hom(FA, HB)
    ~=              ~=
Hom(A, HGB)     Hom(A, GHB)

So there are two ways to compose the adjunctions, giving two induced adjunctions:

FG ⊣ HG,  GF ⊣ GH

And there is something special about these adjunctions. Note that FG is the comonad for the F ⊣ G adjunction, while HG is the monad for the G ⊣ H adjunction. Similarly, GF is the F ⊣ G monad, and GH is the G ⊣ H comonad. So each adjoint triple gives rise to two adjunctions between monads and comonads.

The second of these has another interesting property. We often want to consider the algebras of a monad, and coalgebras of a comonad. The (co)algebra operations with carrier A have type:

alg   : GFA -> A
coalg : A -> GHA

but these types are isomorphic according to the GF ⊣ GH adjunction. Thus, one might guess that GF monad algebras are also GH comonad coalgebras, and that in such a situation, we actually have some structure that can be characterized both ways. In fact this is true for any monad left adjoint to a comonad; [0] but all adjoint triples give rise to these.

The first adjunction actually turns out to be more familiar for the triple examples above, though. (Edit: [2]) If we consider the Σ ⊣ Const ⊣ Π adjunction, where:

Σ Π : (A -> Type) -> Type
Const : Type -> (A -> Type)

we get:

ΣConst : Type -> Type
ΣConst B = A × B
ΠConst : Type -> Type
ΠConst B = A -> B

So this is the familiar adjunction:

A × - ⊣ A -> -

But, there happens to be a triple that is a bit more interesting for both cases. It refers back to categories of functors vs. bare type constructors mentioned in previous posts. So, suppose we have a category called Con whose objects are (partially applied) type constructors (f, g) with kind * -> *, and arrows are polymorphic functions with types like:

 
forall x. f x -> g x
 

And let us further imagine that there is a similar category, called Func, except its objects are the things with Functor instances. Now, there is a functor:

U : Func -> Con

that 'forgets' the functor instance requirement. This functor is in the middle of an adjoint triple:

F ⊣ U ⊣ C
F, C : Con -> Func

where F creates the free functor over a type constructor, and C creates the cofree functor over a type constructor. These can be written using the types:

 
data F f a = forall e. F (e -> a) (f e)
newtype C f a = C (forall r. (a -> r) -> f r)
 

and these types will also serve as the types involved in the composite adjunctions:

FU ⊣ CU : Func -> Func
UF ⊣ UC : Con -> Con

Now, CU is a monad on functors, and the Yoneda lemma tells us that it is actually the identity monad. Similarly, FU is a comonad, and the co-Yoneda lemma tells us that it is the identity comonad (which makes sense, because identity is self-adjoint; and the above is why F and C are often named (Co)Yoneda in Haskell examples).

On the other hand, UF is a monad on type constructors (note, U isn't represented in the Haskell types; F and C just play triple duty, and the constraints on f control what's going on):

 
eta :: f a -> F f a
eta = F id
 
transform :: (forall x. f x -> g x) -> F f a -> F g a
transform tr (F g x) = F g (tr x)
 
mu :: F (F f) a -> F f a
mu (F g (F h x)) = F (g . h) x
 

and UC is a comonad:

 
epsilon :: C f a -> f a
epsilon (C e) = e id
 
transform' :: (forall x. f x -> g x) -> C f a -> C g a
transform' tr (C e) = C (tr . e)
 
delta :: C f a -> C (C f) a
delta (C e) = C $ \h -> C $ \g -> e (g . h)
 

These are not the identity (co)monad, but this is the case where we have algebras and coalgebras that are equivalent. So, what are the (co)algebras? If we consider UF (and unpack the definitions somewhat):

 
alg :: forall e. (e -> a, f e) -> f a
alg (id, x) = x
alg (g . h, x) = alg (g, alg (h, x))
 

and for UC:

 
coalg :: f a -> forall r. (a -> r) -> f r
coalg x id = x
coalg x (g . h) = coalg (coalg x h) g
 

in other words, (co)algebra actions of these (co)monads are (mangled) fmap implementations, and the commutativity requirements are exactly what is required to be a law abiding instance. So the (co)algebras are exactly the Functors. [1]

There are, of course, many other examples of adjoint triples. And further, there are even adjoint quadruples, which in turn give rise to adjoint triples of (co)monads. Hopefully this has sparked some folks' interest in finding and studying more interesting examples.

[0]: Another exmaple is A × - ⊣ A -> - where the A in question is a monoid. (Co)monad (co)algebras of these correspond to actions of the monoid on the carrier set.

[1]: This shouldn't be too surprising, because having a category of (co)algebraic structures that is equivalent to the category of (co)algebras of the (co)monad that comes from the (co)free-forgetful adjunction is the basis for doing algebra in category theory (with (co)monads, at least). However, it is somewhat unusual for a forgetful functor to have both a left and right adjoint. In many cases, something is either algebraic or coalgebraic, and not both.

[2]: Urs Schreiber informed me of an interesting interpretation of the ConstΣ ⊣ ConstΠ adjunction. If you are familiar with modal logic and the possible worlds semantics thereof, you can probably imagine that we could model it using something like P : W -> Type, where W is the type of possible worlds, and propositions are types. Then values of type Σ P demonstrate that P holds in particular worlds, while values of type Π P demonstrate that it holds in all worlds. Const turns these types back into world-indexed 'propositions,' so ConstΣ is the possibility modality and ConstΠ is the necessity modality.

In the last couple posts I've used some 'free' constructions, and not remarked too much on how they arise. In this post, I'd like to explore them more. This is going to be something of a departure from the previous posts, though, since I'm not going to worry about thinking precisely about bottom/domains. This is more an exercise in applying some category theory to Haskell, "fast and loose".

(Advance note: for some continuous code to look at see this file.)

First, it'll help to talk about how some categories can work in Haskell. For any kind k made of * and (->), [0] we can define a category of type constructors. Objects of the category will be first-class [1] types of that kind, and arrows will be defined by the following type family:

 
newtype Transformer f g = Transform { ($$) :: forall i. f i ~> g i }
 
type family (~>) :: k -> k -> * where
  (~>) = (->)
  (~>) = Transformer
 
type a < -> b = (a -> b, b -> a)
type a < ~> b = (a ~> b, b ~> a)
 

So, for a base case, * has monomorphic functions as arrows, and categories for higher kinds have polymorphic functions that saturate the constructor:

 
  Int ~> Char = Int -> Char
  Maybe ~> [] = forall a. Maybe a -> [a]
  Either ~> (,) = forall a b. Either a b -> (a, b)
  StateT ~> ReaderT = forall s m a. StateT s m a -> ReaderT s m a
 

We can of course define identity and composition for these, and it will be handy to do so:

 
class Morph (p :: k -> k -> *) where
  id :: p a a
  (.) :: p b c -> p a b -> p a c
 
instance Morph (->) where
  id x = x
  (g . f) x = g (f x)
 
instance Morph ((~>) :: k -> k -> *)
      => Morph (Transformer :: (i -> k) -> (i -> k) -> *) where
  id = Transform id
  Transform f . Transform g = Transform $ f . g
 

These categories can be looked upon as the most basic substrates in Haskell. For instance, every type of kind * -> * is an object of the relevant category, even if it's a GADT or has other structure that prevents it from being nicely functorial.

The category for * is of course just the normal category of types and functions we usually call Hask, and it is fairly analogous to the category of sets. One common activity in category theory is to study categories of sets equipped with extra structure, and it turns out we can do this in Haskell, as well. And it even makes some sense to study categories of structures over any of these type categories.

When we equip our types with structure, we often use type classes, so that's how I'll do things here. Classes have a special status socially in that we expect people to only define instances that adhere to certain equational rules. This will take the place of equations that we are not able to state in the Haskell type system, because it doesn't have dependent types. So using classes will allow us to define more structures that we normally would, if only by convention.

So, if we have a kind k, then a corresponding structure will be σ :: k -> Constraint. We can then define the category (k,σ) as having objects t :: k such that there is an instance σ t. Arrows are then taken to be f :: t ~> u such that f "respects" the operations of σ.

As a simple example, we have:

 
  k = *
  σ = Monoid :: * -> Constraint
 
  Sum Integer, Product Integer, [Integer] :: (*, Monoid)
 
  f :: (Monoid m, Monoid n) => m -> n
    if f mempty = mempty
       f (m <> n) = f m <> f n
 

This is just the category of monoids in Haskell.

As a side note, we will sometimes be wanting to quantify over these "categories of structures". There isn't really a good way to package together a kind and a structure such that they work as a unit, but we can just add a constraint to the quantification. So, to quantify over all Monoids, we'll use 'forall m. Monoid m => ...'.

Now, once we have these categories of structures, there is an obvious forgetful functor back into the unadorned category. We can then look for free and cofree functors as adjoints to this. More symbolically:

 
  Forget σ :: (k,σ) -> k
  Free   σ :: k -> (k,σ)
  Cofree σ :: k -> (k,σ)
 
  Free σ ⊣ Forget σ ⊣ Cofree σ
 

However, what would be nicer (for some purposes) than having to look for these is being able to construct them all systematically, without having to think much about the structure σ.

Category theory gives a hint at this, too, in the form of Kan extensions. In category terms they look like:

  p : C -> C'
  f : C -> D
  Ran p f : C' -> D
  Lan p f : C' -> D

  Ran p f c' = end (c : C). Hom_C'(c', p c) ⇒ f c
  Lan p f c' = coend (c : c). Hom_C'(p c, c') ⊗ f c

where ⇒ is a "power" and ⊗ is a copower, which are like being able to take exponentials and products by sets (or whatever the objects of the hom category are), instead of other objects within the category. Ends and coends are like universal and existential quantifiers (as are limits and colimits, but ends and coends involve mixed-variance).

Some handy theorems relate Kan extensions and adjoint functors:

  if L ⊣ R
  then L = Ran R Id and R = Lan L Id

  if Ran R Id exists and is absolute
  then Ran R Id ⊣ R

  if Lan L Id exists and is absolute
  then L ⊣ Lan L Id

  Kan P F is absolute iff forall G. (G . Kan P F) ~= Kan P (G . F)

It turns out we can write down Kan extensions fairly generally in Haskell. Our restricted case is:

 
  p = Forget σ :: (k,σ) -> k
  f = Id :: (k,σ) -> (k,σ)
 
  Free   σ = Ran (Forget σ) Id :: k -> (k,σ)
  Cofree σ = Lan (Forget σ) Id :: k -> (k,σ)
 
  g :: (k,σ) -> j
  g . Free   σ = Ran (Forget σ) g
  g . Cofree σ = Lan (Forget σ) g
 

As long as the final category is like one of our type constructor categories, ends are universal quantifiers, powers are function types, coends are existential quantifiers and copowers are product spaces. This only breaks down for our purposes when g is contravariant, in which case they are flipped. For higher kinds, these constructions occur point-wise. So, we can break things down into four general cases, each with cases for each arity:

 
newtype Ran0 σ p (f :: k -> *) a =
  Ran0 { ran0 :: forall r. σ r => (a ~> p r) -> f r }
 
newtype Ran1 σ p (f :: k -> j -> *) a b =
  Ran1 { ran1 :: forall r. σ r => (a ~> p r) -> f r b }
 
-- ...
 
data RanOp0 σ p (f :: k -> *) a =
  forall e. σ e => RanOp0 (a ~> p e) (f e)
 
-- ...
 
data Lan0 σ p (f :: k -> *) a =
  forall e. σ e => Lan0 (p e ~> a) (f e)
 
data Lan1 σ p (f :: k -> j -> *) a b =
  forall e. σ e => Lan1 (p e ~> a) (f e b)
 
-- ...
 
data LanOp0 σ p (f :: k -> *) a =
  LanOp0 { lan0 :: forall r. σ r => (p r -> a) -> f r }
 
-- ...
 

The more specific proposed (co)free definitions are:

 
type family Free   :: (k -> Constraint) -> k -> k
type family Cofree :: (k -> Constraint) -> k -> k
 
newtype Free0 σ a = Free0 { gratis0 :: forall r. σ r => (a ~> r) -> r }
type instance Free = Free0
 
newtype Free1 σ f a = Free1 { gratis1 :: forall g. σ g => (f ~> g) -> g a }
type instance Free = Free1
 
-- ...
 
data Cofree0 σ a = forall e. σ e => Cofree0 (e ~> a) e
type instance Cofree = Cofree0
 
data Cofree1 σ f a = forall g. σ g => Cofree1 (g ~> f) (g a)
type instance Cofree = Cofree1
 
-- ...
 

We can define some handly classes and instances for working with these types, several of which generalize existing Haskell concepts:

 
class Covariant (f :: i -> j) where
  comap :: (a ~> b) -> (f a ~> f b)
 
class Contravariant f where
  contramap :: (b ~> a) -> (f a ~> f b)
 
class Covariant m => Monad (m :: i -> i) where
  pure :: a ~> m a
  join :: m (m a) ~> m a
 
class Covariant w => Comonad (w :: i -> i) where
  extract :: w a ~> a
  split :: w a ~> w (w a)
 
class Couniversal σ f | f -> σ where
  couniversal :: σ r => (a ~> r) -> (f a ~> r)
 
class Universal σ f | f -> σ where
  universal :: σ e => (e ~> a) -> (e ~> f a)
 
instance Covariant (Free0 σ) where
  comap f (Free0 e) = Free0 (e . (.f))
 
instance Monad (Free0 σ) where
  pure x = Free0 $ \k -> k x
  join (Free0 e) = Free0 $ \k -> e $ \(Free0 e) -> e k
 
instance Couniversal σ (Free0 σ) where
  couniversal h (Free0 e) = e h
 
-- ...
 

The only unfamiliar classes here should be (Co)Universal. They are for witnessing the adjunctions that make Free σ the initial σ and Cofree σ the final σ in the relevant way. Only one direction is given, since the opposite is very easy to construct with the (co)monad structure.

Free σ is a monad and couniversal, Cofree σ is a comonad and universal.

We can now try to convince ourselves that Free σ and Cofree σ are absolute Here are some examples:

 
free0Absolute0 :: forall g σ a. (Covariant g, σ (Free σ a))
               => g (Free0 σ a) < -> Ran σ Forget g a
free0Absolute0 = (l, r)
 where
 l :: g (Free σ a) -> Ran σ Forget g a
 l g = Ran0 $ \k -> comap (couniversal $ remember0 . k) g
 
 r :: Ran σ Forget g a -> g (Free σ a)
 r (Ran0 e) = e $ Forget0 . pure
 
free0Absolute1 :: forall (g :: * -> * -> *) σ a x. (Covariant g, σ (Free σ a))
               => g (Free0 σ a) x < -> Ran σ Forget g a x
free0Absolute1 = (l, r)
 where
 l :: g (Free σ a) x -> Ran σ Forget g a x
 l g = Ran1 $ \k -> comap (couniversal $ remember0 . k) $$ g
 
 r :: Ran σ Forget g a x -> g (Free σ a) x
 r (Ran1 e) = e $ Forget0 . pure
 
free0Absolute0Op :: forall g σ a. (Contravariant g, σ (Free σ a))
                 => g (Free0 σ a) < -> RanOp σ Forget g a
free0Absolute0Op = (l, r)
 where
 l :: g (Free σ a) -> RanOp σ Forget g a
 l = RanOp0 $ Forget0 . pure
 
 r :: RanOp σ Forget g a -> g (Free σ a)
 r (RanOp0 h g) = contramap (couniversal $ remember0 . h) g
 
-- ...
 

As can be seen, the definitions share a lot of structure. I'm quite confident that with the right building blocks these could be defined once for each of the four types of Kan extensions, with types like:

 
freeAbsolute
  :: forall g σ a. (Covariant g, σ (Free σ a))
  => g (Free σ a) < ~> Ran σ Forget g a
 
cofreeAbsolute
  :: forall g σ a. (Covariant g, σ (Cofree σ a))
  => g (Cofree σ a) < ~> Lan σ Forget g a
 
freeAbsoluteOp
  :: forall g σ a. (Contravariant g, σ (Free σ a))
  => g (Free σ a) < ~> RanOp σ Forget g a
 
cofreeAbsoluteOp
  :: forall g σ a. (Contravariant g, σ (Cofree σ a))
  => g (Cofree σ a) < ~> LanOp σ Forget g a
 

However, it seems quite difficult to structure things in a way such that GHC will accept the definitions. I've successfully written freeAbsolute using some axioms, but turning those axioms into class definitions and the like seems impossible.

Anyhow, the punchline is that we can prove absoluteness using only the premise that there is a valid σ instance for Free σ and Cofree σ. This tends to be quite easy; we just borrow the structure of the type we are quantifying over. This means that in all these cases, we are justified in saying that Free σ ⊣ Forget σ ⊣ Cofree σ, and we have a very generic presentations of (co)free structures in Haskell. So let's look at some.

We've already seen Free Monoid, and last time we talked about Free Applicative, and its relation to traversals. But, Applicative is to traversal as Functor is to lens, so it may be interesting to consider constructions on that. Both Free Functor and Cofree Functor make Functors:

 
instance Functor (Free1 Functor f) where
  fmap f (Free1 e) = Free1 $ fmap f . e
 
instance Functor (Cofree1 Functor f) where
  fmap f (Cofree1 h e) = Cofree1 h (fmap f e)
 

And of course, they are (co)monads, covariant functors and (co)universal among Functors. But, it happens that I know some other types with these properties:

 
data CoYo f a = forall e. CoYo (e -> a) (f e)
 
instance Covariant CoYo where
  comap f = Transform $ \(CoYo h e) -> CoYo h (f $$ e)
 
instance Monad CoYo where
  pure = Transform $ CoYo id
  join = Transform $ \(CoYo h (CoYo h' e)) -> CoYo (h . h') e
 
instance Functor (CoYo f) where
  fmap f (CoYo h e) = CoYo (f . h) e
 
instance Couniversal Functor CoYo where
  couniversal tr = Transform $ \(CoYo h e) -> fmap h (tr $$ e)
 
newtype Yo f a = Yo { oy :: forall r. (a -> r) -> f r }
 
instance Covariant Yo where
  comap f = Transform $ \(Yo e) -> Yo $ (f $$) . e
 
instance Comonad Yo where
  extract = Transform $ \(Yo e) -> e id
  split = Transform $ \(Yo e) -> Yo $ \k -> Yo $ \k' -> e $ k' . k
 
instance Functor (Yo f) where
  fmap f (Yo e) = Yo $ \k -> e (k . f)
 
instance Universal Functor Yo where
  universal tr = Transform $ \e -> Yo $ \k -> tr $$ fmap k e
 

These are the types involved in the (co-)Yoneda lemma. CoYo is a monad, couniversal among functors, and CoYo f is a Functor. Yo is a comonad, universal among functors, and is always a Functor. So, are these equivalent types?

 
coyoIso :: CoYo < ~> Free Functor
coyoIso = (Transform $ couniversal pure, Transform $ couniversal pure)
 
yoIso :: Yo < ~> Cofree Functor
yoIso = (Transform $ universal extract, Transform $ universal extract)
 

Indeed they are. And similar identities hold for the contravariant versions of these constructions.

I don't have much of a use for this last example. I suppose to be perfectly precise, I should point out that these uses of (Co)Yo are not actually part of the (co-)Yoneda lemma. They are two different constructions. The (co-)Yoneda lemma can be given in terms of Kan extensions as:

 
yoneda :: Ran Id f < ~> f
 
coyoneda :: Lan Id f < ~> f
 

But, the use of (Co)Yo to make Functors out of things that aren't necessarily is properly thought of in other terms. In short, we have some kind of category of Haskell types with only identity arrows---it is discrete. Then any type constructor, even non-functorial ones, is certainly a functor from said category (call it Haskrete) into the normal one (Hask). And there is an inclusion functor from Haskrete into Hask:

             F
 Haskrete -----> Hask
      |        /|
      |       /
      |      /
Incl  |     /
      |    /  Ran/Lan Incl F
      |   /
      |  /
      v /
    Hask

So, (Co)Free Functor can also be thought of in terms of these Kan extensions involving the discrete category.

To see more fleshed out, loadable versions of the code in this post, see this file. I may also try a similar Agda development at a later date, as it may admit the more general absoluteness constructions easier.

[0]: The reason for restricting ourselves to kinds involving only * and (->) is that they work much more simply than data kinds. Haskell values can't depend on type-level entities without using type classes. For *, this is natural, but for something like Bool -> *, it is more natural for transformations to be able to inspect the booleans, and so should be something more like forall b. InspectBool b => f b -> g b.

[1]: First-class types are what you get by removing type families and synonyms from consideration. The reason for doing so is that these can't be used properly as parameters and the like, except in cases where they reduce to some other type that is first-class. For example, if we define:

 
type I a = a
 

even though GHC will report I :: * -> *, it is not legal to write Transform I I.

The following letter is not about what "old hands" know and newcomers do not. Instead, it is about lessons that we all need to learn more than once, and remind ourselves of. It is about tendencies that are common, and understandable, and come with the flush of excitement of learning any new thing that we understand is important, and about the difficulty, always, in trying to decide how best to convey that excitement and sense of importance to others, in a way that they will listen. It is written more specifically, but only because I have found that if we don't talk specifics as well as generalities, the generalities make no sense. This holds for algebraic structures, and it holds for other, vaguer concepts no less. It is a letter full of things I want to remember, as well as of advice I want to share. I expect I will want to remind myself of it when I encounter somebody who is wrong on the internet, which, I understand, may occur on rare occasion.

You’ve recently entered the world of strongly typed functional programming, and you’ve decided it is great. You’ve written a program or two or a library or two, and you’re getting the hang of it. You hop on IRC and hear new words and ideas every day. There are always new concepts to learn, new libraries to explore, new ways to refactor your code, new typeclasses to make instances of.

Now, you’re a social person, and you want to go forth and share all the great things you’ve learned. And you have learned enough to distinguish some true statements from some false statements, and you want to go and slay all the false statements in the world.

Is this really what you want to do? Do you want to help people, do you want to teach people new wonderful things? Do you want to share the things that excite you? Or do you want to feel better about yourself, confirm that you are programming better, confirm that you are smarter and know more, reassure yourself that your adherence to a niche language is ok by striking out against the mainstream? Of course, you want to do the former. But a part of you probably secretly wants to do the latter, because in my experience that part is in all of us. It is our ego, and it drives us to great things, but it also can hold us back, make us act like jerks, and, worst of all, stand in the way of communicating with others about what we truly care about.

Haskell wasn’t built on great ideas, although it has those. It was built on a culture of how ideas are treated. It was not built on slaying others’ dragons, but on finding our own way; not tearing down rotten ideas (no matter how rotten) but showing by example how we didn’t need those ideas after all.

In functional programming, our proofs are not by contradiction, but by construction. If you want to teach functional programming, or preach functional programming, or just to even have productive discussions as we all build libraries and projects together, it will serve you well to learn that ethic.

You know better than the next developer, or so you think. This is because of something you have learned. So how do you help them want to learn it too? You do not tell them this is a language for smart people. You do not tell them you are smart because you use this language. You tell them that types are for fallible people, like we all are. They help us reason and catch our mistakes, because while software has grown more complex, we’re still stuck with the same old brains. If they tell you they don’t need types to catch errors, tell them that they must be much smarter than you, because you sure do. But even more, tell them that all the brainpower they use to not need types could turn into even greater, bigger, and more creative ideas if they let the compiler help them.

This is not a language for clever people, although there are clever things that can be done in this language. It is a language for simple things and clever things alike, and sometimes we want to be simple, and sometimes we want to be clever. But we don’t give bonus points for being clever. Sometimes, it’s just fun, like solving a crossword puzzle or playing a tricky Bach prelude, or learning a tango. We want to keep simple things simple so that tricky things are possible.

It is not a language that is “more mathematical” or “for math” or “about math”. Yes, in a deep formal sense, programming is math. But when someone objects to this, this is not because they are a dumb person, a bad person, or a malicious person. They object because they have had a bad notion of math foisted on them. “Math” is the thing that people wield over them to tell them they are not good enough, that they cannot learn things, that they don’t have the mindset for it. That’s a dirty lie. Math is not calculation — that’s what computers are for. Nor is math just abstract symbols. Nor is math a prerequisite for Haskell. If anything, Haskell might be what makes somebody find math interesting at all. Our equation should not be that math is hard, and so programming is hard. Rather, it should be that programming can be fun, and this means that math can be fun too. Some may object that programming is not only math, because it is engineering as well, and creativity, and practical tradeoffs. But, surprisingly, these are also elements of the practice of math, if not the textbooks we are given.

I have known great Haskell programmers, and even great computer scientists who know only a little linear algebra maybe, or never bothered to pick up category theory. You don’t need that stuff to be a great Haskell programmer. It might be one way. The only thing you need category theory for is to take great categorical and mathematical concepts from the world and import them back to programming, and translate them along the way so that others don’t need to make the same journey you did. And you don’t even need to do that, if you have patience, because somebody else will come along and do it for you, eventually.

The most important thing, though not hardest, about teaching and spreading knowledge is to emphasize that this is for everyone. Nobody is too young, too inexperienced, too old, too set in their ways, too excitable, insufficiently mathematical, etc. Believe in everyone, attack nobody, even the trolliest.* Attacking somebody builds a culture of sniping and argumentativeness. It spreads to the second trolliest, and soforth, and then eventually to an innocent bystander who just says the wrong thing to spark bad memories of the last big argument.

The hardest thing, and the second most important, is to put aside your pride. If you want to teach people, you have to empathize with how they think, and also with how they feel. If your primary goal is to spread knowledge, then you must be relentlessly self-critical of anything you do or say that gets in the way of that. And you don’t get to judge that — others do. And you must just believe them. I told you this was hard. So if somebody finds you offputting, that’s your fault. If you say something and somebody is hurt or takes offense, it is not their fault for being upset, or feeling bad. This is not about what is abstractly hurtful in a cosmic sense; it is about the fact that you have failed, concretely, to communicate as you desired. So accept the criticism, apologize for giving offense (not just for having upset someone but also for what you did to hurt them), and attempt to learn why they feel how they feel, for next time.

Note that if you have made somebody feel crummy, they may not be in a mood to explain why or how, because their opinion of you has already plummeted. So don’t declare that they must or should explain themselves to you, although you may politely ask. Remember that knowledge does not stand above human behavior. Often, you don't need to know exactly why a person feels the way they do, only that they do, so you can respect that. If you find yourself demanding explanations, ask yourself, if you knew this thing, would that change your behavior? How? If not, then learn to let it go.

Remember also that they were put off by your actions, not by your existence. It is easy to miss this distinction and react defensively. "Fight-or-flight" stands in the way of clear thinking and your ability to empathize; try taking a breath and maybe a walk until the adrenaline isn't derailing your true intentions.

Will this leave you satisfied? That depends. If your goal is to understand everything and have everybody agree with regards to everything that is in some sense objectively true, it will not. If your goal is to have the widest, nicest, most diverse, and most fun Haskell community possible, and to interact in an atmosphere of mutual respect and consideration, then it is the only thing that will leave you satisfied.

If you make even the most modest (to your mind) mistake, be it in social interaction or technical detail, be quick to apologize and retract, and do so freely. What is there to lose? Only your pride. Who keeps track? Only you. What is there to gain? Integrity, and ultimately that integrity will feel far more fulfilling than the cheap passing thrills of cutting somebody else down or deflecting their concerns.

Sometimes it may be, for whatever reason, that somebody doesn’t want to talk to you, because at some point your conversation turned into an argument. Maybe they did it, maybe you did it, maybe you did it together. It doesn’t matter, learn to walk away. Learn from the experience how to communicate better, how to avoid that pattern, how to always be the more positive, more friendly, more forward-looking. Take satisfaction in the effort in that. Don’t talk about them behind their back, because that will only fuel your own bad impulses. Instead, think about how you can change.

Your self-esteem doesn’t need your help. You may feel you need to prove yourself, but you don't. Other people, in general, have better things to do with their time than judge you, even when you may sometimes feel otherwise. You know you’re talented, that you have learned things, and built things, and that this will be recognized in time. Nobody else wants to hear it from you, and the more they hear it, the less they will believe it, and the more it will distract from what you really want, which is not to feed your ego, not to be great, but to accomplish something great, or even just to find others to share something great with. In fact, if anyone's self-esteem should be cared for, it is that of the people you are talking to. The more confident they are in their capacity and their worth, the more willing they will be to learn new things, and to acknowledge that their knowledge, like all of ours, is limited and partial. You must believe in yourself to be willing to learn new things, and if you want to cultivate more learners, you must cultivate that self-belief in others.

Knowledge is not imposing. Knowledge is fun. Anyone, given time and inclination, can acquire it. Don’t only lecture, but continue to learn, because there is always much more than you know. (And if there wasn’t, wow, that would be depressing, because what would there be to learn next?) Learn to value all opinions, because they all come from experiences, and all those experiences have something to teach us. Dynamic typing advocates have brought us great leaps in JIT techniques. If you’re interested in certain numerical optimizations, you need to turn to work pioneered in C++ or Fortran. Like you, I would rather write in Haskell. But it is not just the tools that matter but the ideas, and you will find they come from everywhere.

In fact, we have so much to learn that we direct our learning by setting up barriers — declaring certain tools, fields, languages, or communities not worth our time. This isn’t because they have nothing to offer, but it is a crutch for us to shortcut evaluating too many options all at once. It is fine, and in fact necessary, to narrow the scope of your knowledge to increase its depth. But be glad that others are charting other paths! Who knows what they will bring back from those explorations.

If somebody is chatting about programming on the internet, they’re already ahead of the pack, already interested in craft and knowledge. You may not share their opinions, but you have things to learn from one another, always. Maybe the time and place aren’t right to share ideas and go over disputes. That’s ok. There will be another time and place, or maybe there won’t be. There is a big internet full of people, and you don’t need to be everybody’s friend or everybody’s mentor. You should just avoid being anybody’s enemy, because your time and theirs is too precious to waste it on hard feelings instead of learning new cool stuff.

This advice is not a one-time proposition. Every time we learn something new and want to share it, we face these issues all over again -- the desire to proclaim, to overturn received wisdom all at once -- and the worse the received wisdom, the more vehemently we want to strike out. But if we are generous listeners and attentive teachers, we not only teach better and spread more knowledge, but also learn more, and enjoy ourselves more in the process. To paraphrase Rilke’s “Letter to a Young Poet”: Knowledge is good if it has sprung from necessity. In this nature of its origin lies the judgement of it: there is no other.

Thanks to the various folks in and around the Haskell world who have helped me refine this article. I don't name you only because I don't want to imply your endorsement, or give what is still, at base, a very personal take, any particular sort of imprimatur of a broader group of people, all of whom I suspect will disagree among themselves and with me about various specifics.

*: It has been pointed out to me that this advice is not universal. Clearly there are some things that deserve more pointed responses. Bigotry, outright harassment and poisonous behavior, etc. So please read this paragraph only as it applies to talking about technical issues, not as regards to many other things, where there are people better equipped than me to give advice.

In the previous two posts, we've built up a whole range of applicatives, out of Const, Identity, Reader, Compose, Product, Sum, and Fix (and some higher-order analogues). Sum has given us the most trouble, but in some sense has been the most powerful, letting us write things like possibly eventually terminating lists, or trees, or in fact any sort of structure with branching alternatives. In this post, I want to think a bit more about why it is that Sum is the trickiest of the bunch, and more generally, what we can say about when two applicative structures are the "same". In the process of doing so, we'll invent something a lot like Traversable en passant.

Let's do some counting exercises. Product Identity Identity holds exactly two things. It is therefore isomorphic to ((->) Bool), or if we prefer, ((->) Either () ()). That is to say that a pair that holds two values of type a is the same as a function that takes a two-valued type and yields a value of type a. A product of more functors in turn is isomorphic to the reader of the sum of each of the datatypes that "represent" them. E.g. Product (Product Identity Identity) (Product (Const ()) Identity) is iso to ((->) (Either (Either () ()) ()), i.e. a data type with three possible inhabitants. In making this move we took Product to Either -- multiplication to sum. We can pull a similar trick with Compose. Compose (Product Identity Identity) (Product Identity Identity) goes to ((->) (Either () (),Either () ())). So again we took Product to a sum type, but now we took Compose to a pair -- a product type! The intuition is that composition multiplies the possibilities of spaces in each nested functor.

Hmm.. products go to sums, composition goes to multiplication, etc. This should remind us of something -- these rules are exactly the rules for working with exponentials. x^n * x^m = x^(n + m). (x^n)^m = x^(n*m). x^0 = 1, x^1 = x.

Seen from the right standpoint, this isn't surprising at all, but almost inevitable. The functors we're describing are known as "representable," a term which derives from category theory. (See appendix on representable functors below).

In Haskell-land, a "representable functor" is just any functor isomorphic to the reader functor ((->) a) for some appropriate a. Now if we think back to our algebraic representations of data types, we call the arrow type constructor an exponential. We can "count" a -> x as x^a, since e.g. there are 3^2 distinct functions that inhabit the type 2 -> 3. The intuition for this is that for each input we pick one of the possible results, so as the number of inputs goes up by one, the number of functions goes up by multiplying through by the set of possible results. 1 -> 3 = 3, 2 -> 3 = 3 * 3, (n + 1) -> 3 = 3 * (n -> 3).

Hence, if we "represent" our functors by exponentials, then we can work with them directly as exponentials as well, with all the usual rules. Edward Kmett has a library encoding representable functors in Haskell.

Meanwhile, Peter Hancock prefers to call such functors "Naperian" after John Napier, inventor of the logarithm (See also here). Why Naperian? Because if our functors are isomorphic to exponentials, then we can take their logs! And that brings us back to the initial discussion of type mathematics. We have some functor F, and claim that it is isomorphic to -^R for some concrete data type R. Well, this means that R is the logarithm of F. E.g. (R -> a, S -> a) =~ Either R S -> a, which is to say that if log F = R and log G =~ S, then log (F * G) = log F + log G. Similarly, for any other data type n, again with log F = R, we have n -> F a =~ n -> R -> a =~ (n * R) -> a, which is to say that log (F^n) =~ n * log F.

This gives us one intuition for why the sum functor is not generally representable -- it is very difficult to decompose log (F + G) into some simpler compound expression of logs.

So what functors are Representable? Anything that can be seen as a fixed shape with some index. Pairs, fixed-size vectors, fixed-size matrices, any nesting of fixed vectors and matricies. But also infinite structures of regular shape! However, not things whose shape can vary -- not lists, not sums. Trees of fixed depth or infinite binary trees therefore, but not trees of arbitrary depth or with ragged structure, etc.

Representable functors turn out to be extremely powerful tools. Once we know a functor is representable, we know exactly what its applicative instance must be, and that its applicative instance will be "zippy" -- i.e. acting pointwise across the structure. We also know that it has a monad instance! And, unfortunately, that this monad instance is typically fairly useless (in that it is also "zippy" -- i.e. the monad instance on a pair just acts on the two elements pointwise, without ever allowing anything in the first slot to affect anything in the second slot, etc.). But we know more than that. We know that a representable functor, by virtue of being a reader in disguise, cannot have effects that migrate outwards. So any two actions in a representable functor are commutative. And more than that, they are entirely independent.

This means that all representable functors are "distributive"! Given any functor f, and any data type r, then we have

 
distributeReader :: Functor f => f (r -> a) -> (r -> f a)
distributeReader fra = \r -> fmap ($r) fra
 

That is to say, given an arrow "inside" a functor, we can always pull the arrow out, and "distribute" application across the contents of the functor. A list of functions from Int -> Int becomes a single function from Int to a list of Int, etc. More generally, since all representable functors are isomorphic to reader, given g representable, and f any functor, then we have: distribute :: (Functor f, Representable g) => f (g a) -> g (f a).

This is pretty powerful sauce! And if f and g are both representable, then we get the transposition isomorphism, witnessed by flip! That's just the beginning of the good stuff. If we take functions and "unrepresent" them back to functors (i.e. take their logs), then we can do things like move from ((->) Bool) to pairs, etc. Since we're in a pervasively lazy language, we've just created a library for memoization! This is because we've gone from a function to a data structure we can index into, representing each possible argument to this function as a "slot" in the structure. And the laziness pays off because we only need to evaluate the contents of each slot on demand (otherwise we'd have a precomputed lookup table rather than a dynamically-evaluated memo table).

And now suppose we take our representable functor in the form s -> a and paired it with an "index" into that function, in the form of a concrete s. Then we'd be able to step that s forward or backwards and navigate around our structure of as. And this is precisely the Store Comonad! And this in turn gives a characterization of the lens laws.

What this all gives us a tiny taste of, in fact, is the tremendous power of the Yoneda lemma, which, in Haskell, is all about going between values and functions, and in fact captures the important universality and uniqueness properties that make working with representable functors tractable. A further tiny taste of Yoneda comes from a nice blog post by Conal Elliott on memoization.

Extra Credit on Sum Functors

There in fact is a log identity on sums. It goes like this:

log(a + c) = log a + log (1 + c/a)

Do you have a useful computational interpretation of this? I've got the inklings of one, but not much else.

Appendix: Notes on Representable Functors in Hask.

The way to think about this is to take some arbitrary category C, and some category that's basically Set (in our case, Hask. In fact, in our case, C is Hask too, and we're just talking about endofunctors on Hask). Now, we take some functor F : C -> Set, and some A which is an element of C. The set of morphisms originating at A (denoted by Hom(A,-)) constitutes a functor called the "hom functor." For any object X in C, we can "plug it in" to Hom(A,-), to then get the set of all arrows from A to X. And for any morphism X -> Y in C, we can derive a morphism from Hom(A,X) to Hom(A,Y), by composition. This is equivalent to, in Haskell-land, using a function f :: x -> y to send g :: a -> x to a -> y by writing "functionAToY = f . g".

So, for any A in C, we have a hom functor on C, which is C -> Set, where the elements of the resultant Set are homomorphisms in C. Now, we have this other arbitrary functor F, which is also C -> Set. Now, if there is an isomorphism of functors between F, and Hom(A,_), then we say F is "representable". A representable functor is thus one that can be worked with entirely as an appropriate hom-functor.

While the previous post in this series was relatively immediately applicable, this one has constructions I definitely wouldn't recommend in production code. However, they do take us further in exploring the universe of applicative functors, and, more broadly, exploring which data types provide which properties by construcion.

It's well known that if you have any Functor F a, you can take its "fixpoint", creating a structure of infinitely nested Fs, like so. F (F (F (...) ) ) Since we can't have infinite types directly in Haskell, we introduce the Fix newtype:

 
newtype Fix f = Fix (f (Fix f))

This "wraps up" the recursion so that GHC accepts the type. Fix f is a Fix constructor, containing an "f" of Fix f inside. Each in turn expands out, and soforth. Fixpoints of functors have fixedpoints of functors inside 'em. And so on, and so on, ad infinitum.

(Digression: We speak of "algebraic data types" in Haskell. The "algebra" in question is an "F-algebra", and we can build up structures with fixpoints of functors, taking those functors as initial or terminal objects and generating either initial algebras or terminal coalgebras. These latter two concepts coincide in Haskell in the Fix description given above, as greatest and least fixpoints of data types in Haskell turn out to be the same thing. For more background, one can go to Wadler's "Recursive Types for Free," or Jacobs and Rutten's "Tutorial on (Co)Algebras and (Co)Induction" for starters.)

The family of functors built from our friends Const, Sum, Product, and Reader (exponentiation) are known as Polynomial Functors. If we take closure of these with a proper fixpoint construct (that lets us build infinite structures), we get things that are variously known as Containers, Shapely Types, and Strictly Positive types.

One irritating thing is that the fixpoint of a functor as we've written it is no longer itself a functor. The type constructor Fix is of kind (* -> *) -> *, which says it takes an "f" which takes one argument (e.g. "Maybe" or "Identity" or etc.) and returns a proper type (i.e. a value at the type level of kind *).

We want a fixpoint construction that gives back something of kind * -> * — i.e. something that is a type constructor representing a functor, and not just a plain old type. The following does the trick.

 
newtype FixF f a = FixF (f (FixF f) a)
deriving instance (Show (f (FixF f) a)) => Show (FixF f a)

(I learned about FixF from a paper by Ralf Hinze, but I'm sure the origins go back much further).

FixF is of kind ((* -> *) -> * -> *) -> * -> *. It takes the fixpoint of a "second-order Functor" (a Functor that sends a Functor to another Functor, i.e. an endofunctor on the functor category of hask), to recover a standard "first order Functor" back out. This sounds scary, but it isn't once you load it up in ghci and start playing with it. In fact, we've encountered second order functors just recently. Product, Sum, and Compose are all of kind (* -> *) -> (* -> *) -> * -> *. So they all send two functors to a third functor. That means that Product Const, Sum Identity and Compose Maybe are all second-order functors, and things appropriate to take our "second-order fixpoint" of.

Conceptually, "Fix f" took a value with one hole, and we filled that hole with "Fix f" so there was no room for a type parameter. Now we've got an "f" with two holes, the first of which takes a functor, and the second of which is the hole of the resulting functor.

Unlike boring old "Fix", we can write Functor and Applicative instances for "FixF", and they're about as simple and compositional as we could possibly hope.

instance Functor (f (FixF f)) => Functor (FixF f) where
    fmap f (FixF x) = FixF $ fmap f x
 
instance Applicative (f (FixF f)) => Applicative (FixF f) where
    pure x = FixF $ pure x
    (FixF f) < *> (FixF x) = FixF (f < *> x)

But now we run into a new problem! It seems like this "a" parameter is just hanging out there, doing basically nothing. We take our classic functors and embed them in there, and they still only have "one hole" at the value level, so don't actually have any place to put the "a" type we now introduced. For example, we can write the following:

-- FixF . Compose . Just . FixF . Compose $ Nothing
-- > FixF (Compose (Just (FixF (Compose Nothing))))
-- :t FixF (Compose (Just (FixF (Compose Nothing))))
-- > FixF (Compose Maybe) a

We now introduce one new member of our basic constructions — a second order functor that acts like "const" on the type level, taking any functor and returning Identity.

 
newtype Embed (f :: * -> *) a = Embed a deriving (Show)
 
instance Functor (Embed f) where
    fmap f (Embed x) = Embed $ f x
 
instance Applicative (Embed f) where
    pure x = Embed x
    (Embed f) < *> (Embed x) = Embed (f x)

Now we can actually stick functorial values into our fixpoints:

-- FixF $ Embed "hi"
-- > FixF (Embed "hi")
 
-- fmap (++ " world") $ FixF (Embed "hi")
-- > FixF (Embed "hi world")
 
-- FixF . Product (Embed "hi") .
--        FixF . Product (Embed "there") . FixF $ undefined
-- > FixF (Product (Embed "hi")
--   (FixF (Product (Embed "there")
--   (FixF *** Exception: Prelude.undefined

You may have noticed that we seem to be able to use "product" to begin a chain of nested fixpoints, but we don't seem able to stick a "Maybe" in there to stop the chain. And it seems like we're not even "fixing" where we intend to be:

-- :t FixF . Product (Embed "hi") . FixF . Product (Embed "there") . FixF $ undefined
-- > FixF (Product (Embed f)) [Char]

That's because we're applying Product, takes and yields arguments of kind * -> * in a context where we really want to take and yield second-order functors as arguments — things of kind (* -> *) -> * -> *. If we had proper kind polymorphism, "Product" and "ProductF" would be able to collapse (and maybe, soon, they will). But at least in the ghc 7.4.1 that I'm working with, we have to write the same darn thing, but "up a kind".

data ProductF f g (b :: * -> *) a =
      ProductF (f b a) (g b a) deriving Show
 
instance (Functor (f b), Functor (g b)) =>
         Functor (ProductF f g b) where
                fmap f (ProductF x y) = ProductF (fmap f x) (fmap f y)
 
instance (Applicative (f b), Applicative (g b)) =>
         Applicative (ProductF f g b) where
               pure x = ProductF (pure x) (pure x)
              (ProductF f g) < *> (ProductF x y) = ProductF (f < *> x) (g < *> y)

We can now do the following properly.

yy = FixF . ProductF (Embed "foo") $ InL $ Const ()
xx = FixF . ProductF (Embed "bar") . InR .
        FixF . ProductF (Embed "baz") . InL $ Const ()

So we've recovered proper lists in Haskell, as the "second-order fixpoint" of polynomial functors. And the types look right too:

-- :t yy
-- > FixF (ProductF Embed (Sum (Const ()))) [Char]

Because we've built our Applicative instances compositionally, we have an applicative for our list list construction automatically:

-- (++) < $> yy < *> xx
-- > FixF (ProductF (Embed "foobar") (InL (Const ())))

This is precisely the "ZipList" applicative instance. In fact, our applicative instances from this "functor toolkit" are all "zippy" — matching up structure where possible, and "smashing it down" where not. This is because Sum, with its associated natural transformation logic, is the only way to introduce a disjoint choice of shape. Here are some simple examples with Sum to demonstrate:

-- liftA2 (++) (InL (Identity "hi")) $
--      InR (Product (Identity " there") (Const ([12::Int])))
-- > InL (Identity "hi there")
-- liftA2 (++) (InR (Identity "hi")) $ InL (Product (Identity " there") (Const ([12::Int])))
-- > InL (Product (Identity "hi there") (Const [12]))

We're always "smashing" towards the left. So in the first case, that means throwing away half of the pair. In the second case, it means injecting Const mempty into a pair, and then operating with that.

In any case, we now have infinite and possibly infinite branching structures. And not only are they Functors, but they're also Applicatives, and in a way that's uniform and straightforward to reason about.

In the next post, we'll stop building out our vocabulary of "base" Functors (though it's not quite complete) and instead push forward on what else these functors can provide "beyond" Applicative.

By and large, there are two sorts of proof systems that people use (these days) when studying logic: natural deduction, and sequent calculus. I know of at least one other---Hilbert style---but it is older, and the above systems were invented due to dissatisfaction with Hilbert systems (for a programming analogy, Hilbert systems are like programming entirely with combinators (S, K, etc.), rather than a lambda calculus).

Natural Deduction

Probably the best way to categorize the difference, for the purpose of where we're eventually going, is that natural deduction focuses on the ways to build proof terms up from their constituent parts. This comes in the form of introduction and elimination rules for the various propositions. For instance, the rules for conjunction are:

This spartan style gets a bit annoying (in my opinion) for the hypothetical premises of the implication introduction, but this can be solved by adding contexts:

This is the style most commonly adopted for presenting type theories, except we reason about terms with a type, rather than just propositions. The context we added for convenience above also becomes fairly essential for keeping track of variables:

As can be seen, all the rules involve taking terms from the premise and building on them in the conclusion.

Sequent Calculi

The other type of system in question, sequent calculus, looks very similar, but represents a subtle shift in focus for our purposes (sequent calculi are a lot more obviously different when presenting classical logics). First, the inference rules relate sequents, which look a lot like our contextual judgments above, and I'll write them the same way. The difference is that not all rules operate on the conclusion side; some operate just on the context. Generally, introduction rules stay similar to natural deduction (and are called right rules), while elimination rules are replaced by manipulations of the context, and are called left rules. For pairs, we can use the rules:

We could also have two separate left rules:

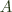But these two different sets are equivalent as long as we're not considering substructural logics. Do note, however, that we're moving from on the top left to 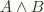on the bottom left, using the fact that is sufficient to imply . That is, projections apply contravariantly to the left.

It turns out that almost no type theory is done in this style; natural deduction is far and away more popular. There are, I think, a few reasons for this. The first is: how do we even extend the left rules to type theory (eliminations are obvious, by contrast)? I know of two ways. The first is to introduce pattern matching into the contexts, so our left rule becomes:

This is an acceptable choice (and may avoid some of the pitfalls in the next option), but it doesn't gel with your typical lambda calculus. It's probably more suited to a pattern calculus of some sort (although, even then, if you want to bend your brain, go look at the left rule for implication and try to figure out how it translates into such a theory; I think you probably need higher-order contexts of some sort). Anyhow, I'm not going to explore this further.

The other option (and one that I've seen in the literature) is that left rules actually involve a variable substitution. So we come up with the following rule:

And with this rule, it becomes (I think) more obvious why natural deduction is preferred over sequent calculus, as implementing this rule in a type checker seems significantly harder. Checking the rules of natural deduction involves examining some outer-most structure of the term, and then checking the constituents of the term, possibly in an augmented context, and which rule we're dealing with is always syntax directed. But this left rule has no syntactic correspondent, so it seems as though we must nondeterministically try all left rules at each step, which is unlikely to result in a good algorithm. This is the same kind of problem that plagues extensional type theory, and ultimately results in only derivations being checkable, not terms.

The Type Class Connection

However, there are certain problems that I believe are well modeled by such a sequent calculus, and one of them is type class checking and associated dictionary translations. This is due mainly to the fact that the process is mainly context-directed term building, rather than term-directed type checking. As far as the type class algorithm goes, there are two interesting cases, having to do with the following two varieties of declaration:

 
  class Eq a => Ord a where ...
  instance (Eq a, Eq b) => Eq (a, b) where ...
 

It turns out that each of these leads to a left rule in a kind of type class sequent calculus:

That is:

1. if Eq a is a sufficient constraint for M : T, then the stronger constraint Ord a is also sufficient, so we can discharge the Eq a constraint and use Ord a instead.
2. We can discharge an Eq (a, b) constraint using two constraints, Eq a, Eq b together with an instance telling us how to do so. This also works for instances without contexts, giving us rules like:

   

Importantly, the type inference algorithm for type classes specifies when we should use these rules based only on the contexts we're dealing with. Now, these look more like the logical sequent rules, but it turns out that they have corresponding type theory-like versions when we consider dictionary passing:

And this kind of substituting into dictionary variables produces exactly the evidence passing translation we want.

Another way to look at the difference in feasibility is that type checking involves moving bottom-to-top across the rules; in natural deduction, this is always easy, and we need look only at the terms to figure out which we should do. Type class checking and dictionary translation moves from top-to-bottom, directed by the left hand context, and produces terms on the right via complex operations, and that is a perfect fit for the sequent calculus rules.

I believe this corresponds to the general opinion on those who have studied sequent calculi with regard to type theory. A quick search revealed mostly papers on proof search, rather than type checking, and type classes rather fall into that realm (they're a very limited form of proof search).

Last time we derived an entailment relation for constraints, now let's get some use out of it.

Reflecting Classes and Instances

Most of the implications we use on a day to day basis come from our class and instance declarations, but last time we only really dealt with constraint products.

(more...)

Max Bolingbroke has done a wonderful job on adding Constraint kinds to GHC.

Constraint Kinds adds a new kind Constraint, such that Eq :: * -> Constraint, Monad :: (* -> *) -> Constraint, but since it is a kind, we can make type families for constraints, and even parameterize constraints on constraints.

So, let's play with them and see what we can come up with!

(more...)

Last time, I showed that we can build a small parsec clone with packrat support.

This time I intend to implement packrat directly on top of Parsec 3.

One of the main topics of discussion when it comes to packrat parsing since Bryan Ford's initial release of Pappy has been the fact that in general you shouldn't use packrat to memoize every rule, and that instead you should apply Amdahl's law to look for the cases where the lookup time is paid back in terms of repetitive evaluation, computation time and the hit rate. This is great news for us, since, we only want to memoize a handful of expensive combinators.

(more...)

You never heard of the Millenium Falcon? It's the ship that made the Kessel Run in 12 parsecs.

I've been working on a parser combinator library called trifecta, and so I decided I'd share some thoughts on parsing.

Packrat parsing (as provided by frisby, pappy, rats! and the Scala parsing combinators) and more traditional recursive descent parsers (like Parsec) are often held up as somehow different.

Today I'll show that you can add monadic parsing to a packrat parser, sacrificing asymptotic guarantees in exchange for the convenient context sensitivity, and conversely how you can easily add packrat parsing to a traditional monadic parser combinator library.

(more...)

Last night, Chung-Chieh Shan posted an example of a pointed-set monad on his blog, which happens to be isomorphic to a non-empty stream monad with a different emphasis.

But, I thought I should point out that the pointed set that he posted also has a comonadic structure, which may be exploited since it is just a variation on the "zipper comonad," a structure that is perhaps more correctly called a "pointing comonad."

(more...)

To those that have asked, I'm still alive.

I had to restore the blog database from a backup and so I lost a few posts, including the index for the various recursion schemes entries. Fortunately, before that happened I had replicated the catamorphism post as a knol.

Should I find myself with a copious glut of free time, I shall happily re-scribe and finish the rest, but I've been very busy.

Does anyone know of any work on "forgetful laziness?"

(more...)

Back in the days of HYLO, it was common to write hylomorphisms with an additional natural transformation in them. Well, I was still coding in evil imperative languages back then, but I have it on reliable, er.. well supposition, that this is probably the case, or at least that they liked to do it back in the HYLO papers anyways.

Transcoding the category theory mumbo-jumbo into Haskell, so I can have a larger audience, we get the following 'frat combinator' -- you can blame Jules Bean from #haskell for that.

 
hyloEta :: Functor f =>
     (g b -> b) ->
     (forall a. f a -> g a) ->
     (a -> f a)
hyloEta phi eta psi = phi . eta . fmap (hyloEta phi eta psi) . psi
 

We placed eta in the middle of the argument list because it is evocative of the fact that it occurs between phi and psi, and because that seems to be where everyone else puts it.

Now, clearly, we could roll eta into phi and get the more traditional hylo where f = g. Less obviously we could roll it into psi because it is a natural transformation and so the following diagram commutes:

This 'Hylo Shift' property (mentioned in that same paper) allows us to move the 'eta' term into the phi term or into the psi term as we see fit. Since we can move the eta term around and it adds no value to the combinator, it quietly returned to the void from whence it came. hyloEta offers us no more power than hylo, so out it goes.

So, if its dead, why talk about it?

(more...)

Wordpress changed the slug of this post, but Planet Haskell has the old link.

Here is the actual content.

Updated my little type-level 2s and 16s complement integer library to be ghc 6.6 friendly and uploaded it to hackage based on popular (er.. ok, well, singular) demand.

O.K. it was more of a polite request, but I did update it.