Last time I looked at free monoids, and noticed that in Haskell lists don't really cut it. This is a consequence of laziness and general recursion. To model a language with those properties, one needs to use domains and monotone, continuous maps, rather than sets and total functions (a call-by-value language with general recursion would use domains and strict maps instead).
This time I'd like to talk about some other examples of this, and point out how doing so can (perhaps) resolve some disagreements that people have about the specific cases.
The first example is not one that I came up with: induction. It's sometimes said that Haskell does not have inductive types at all, or that we cannot reason about functions on its data types by induction. However, I think this is (techincally) inaccurate. What's true is that we cannot simply pretend that that our types are sets and use the induction principles for sets to reason about Haskell programs. Instead, one has to figure out what inductive domains would be, and what their proof principles are.
Fortunately, there are some papers about doing this. The most recent (that I'm aware of) is Generic Fibrational Induction. I won't get too into the details, but it shows how one can talk about induction in a general setting, where one has a category that roughly corresponds to the type theory/programming language, and a second category of proofs that is 'indexed' by the first category's objects. Importantly, it is not required that the second category is somehow 'part of' the type theory being reasoned about, as is often the case with dependent types, although that is also a special case of their construction.
One of the results of the paper is that this framework can be used to talk about induction principles for types that don't make sense as sets. Specifically:
newtype Hyp = Hyp ((Hyp -> Int) -> Int)
the type of "hyperfunctions". Instead of interpreting this type as a set, where it would effectively require a set that is isomorphic to the power set of its power set, they interpret it in the category of domains and strict functions mentioned earlier. They then construct the proof category in a similar way as one would for sets, except instead of talking about predicates as subsets, we talk about sub-domains instead. Once this is done, their framework gives a notion of induction for this type.
This example is suitable for ML (and suchlike), due to the strict functions, and sort of breaks the idea that we can really get away with only thinking about sets, even there. Sets are good enough for some simple examples (like flat domains where we don't care about ⊥), but in general we have to generalize induction itself to apply to all types in the 'good' language.
While I haven't worked out how the generic induction would work out for Haskell, I have little doubt that it would, because ML actually contains all of Haskell's data types (and vice versa). So the fact that the framework gives meaning to induction for ML implies that it does so for Haskell. If one wants to know what induction for Haskell's 'lazy naturals' looks like, they can study the ML analogue of:
data LNat = Zero | Succ (() -> LNat)
because function spaces lift their codomain, and make things 'lazy'.
----
The other example I'd like to talk about hearkens back to the previous article. I explained how foldMap is the proper fundamental method of the Foldable class, because it can be massaged to look like:
foldMap :: Foldable f => f a -> FreeMonoid a
and lists are not the free monoid, because they do not work properly for various infinite cases.
I also mentioned that foldMap looks a lot like traverse:
foldMap :: (Foldable t , Monoid m) => (a -> m) -> t a -> m
traverse :: (Traversable t, Applicative f) => (a -> f b) -> t a -> f (t b)
And of course, we have Monoid m => Applicative (Const m), and the functions are expected to agree in this way when applicable.
Now, people like to get in arguments about whether traversals are allowed to be infinite. I know Ed Kmett likes to argue that they can be, because he has lots of examples. But, not everyone agrees, and especially people who have papers proving things about traversals tend to side with the finite-only side. I've heard this includes one of the inventors of Traversable, Conor McBride.
In my opinion, the above disagreement is just another example of a situation where we have a generic notion instantiated in two different ways, and intuition about one does not quite transfer to the other. If you are working in a language like Agda or Coq (for proving), you will be thinking about traversals in the context of sets and total functions. And there, traversals are finite. But in Haskell, there are infinitary cases to consider, and they should work out all right when thinking about domains instead of sets. But I should probably put forward some argument for this position (and even if I don't need to, it leads somewhere else interesting).
One example that people like to give about finitary traversals is that they can be done via lists. Given a finite traversal, we can traverse to get the elements (using Const [a]), traverse the list, then put them back where we got them by traversing again (using State [a]). Usually when you see this, though, there's some subtle cheating in relying on the list to be exactly the right length for the second traversal. It will be, because we got it from a traversal of the same structure, but I would expect that proving the function is actually total to be a lot of work. Thus, I'll use this as an excuse to do my own cheating later.
Now, the above uses lists, but why are we using lists when we're in Haskell? We know they're deficient in certain ways. It turns out that we can give a lot of the same relevant structure to the better free monoid type:
newtype FM a = FM (forall m. Monoid m => (a -> m) -> m) deriving (Functor)
instance Applicative FM where
pure x = FM ($ x)
FM ef < *> FM ex = FM $ \k -> ef $ \f -> ex $ \x -> k (f x)
instance Monoid (FM a) where
mempty = FM $ \_ -> mempty
mappend (FM l) (FM r) = FM $ \k -> l k <> r k
instance Foldable FM where
foldMap f (FM e) = e f
newtype Ap f b = Ap { unAp :: f b }
instance (Applicative f, Monoid b) => Monoid (Ap f b) where
mempty = Ap $ pure mempty
mappend (Ap l) (Ap r) = Ap $ (<>) < $> l < *> r
instance Traversable FM where
traverse f (FM e) = unAp . e $ Ap . fmap pure . f
So, free monoids are Monoids (of course), Foldable, and even Traversable. At least, we can define something with the right type that wouldn't bother anyone if it were written in a total language with the right features, but in Haskell it happens to allow various infinite things that people don't like.
Now it's time to cheat. First, let's define a function that can take any Traversable to our free monoid:
toFreeMonoid :: Traversable t => t a -> FM a
toFreeMonoid f = FM $ \k -> getConst $ traverse (Const . k) f
Now let's define a Monoid that's not a monoid:
data Cheat a = Empty | Single a | Append (Cheat a) (Cheat a)
instance Monoid (Cheat a) where
mempty = Empty
mappend = Append
You may recognize this as the data version of the free monoid from the previous article, where we get the real free monoid by taking a quotient. using this, we can define an Applicative that's not valid:
newtype Cheating b a =
Cheating { prosper :: Cheat b -> a } deriving (Functor)
instance Applicative (Cheating b) where
pure x = Cheating $ \_ -> x
Cheating f < *> Cheating x = Cheating $ \c -> case c of
Append l r -> f l (x r)
Given these building blocks, we can define a function to relabel a traversable using a free monoid:
relabel :: Traversable t => t a -> FM b -> t b
relabel t (FM m) = propser (traverse (const hope) t) (m Single)
where
hope = Cheating $ \c -> case c of
Single x -> x
And we can implement any traversal by taking a trip through the free monoid:
slowTraverse
:: (Applicative f, Traversable t) => (a -> f b) -> t a -> f (t b)
slowTraverse f t = fmap (relabel t) . traverse f . toFreeMonoid $ t
And since we got our free monoid via traversing, all the partiality I hid in the above won't blow up in practice, rather like the case with lists and finite traversals.
Arguably, this is worse cheating. It relies on the exact association structure to work out, rather than just number of elements. The reason is that for infinitary cases, you cannot flatten things out, and there's really no way to detect when you have something infinitary. The finitary traversals have the luxury of being able to reassociate everything to a canonical form, while the infinite cases force us to not do any reassociating at all. So this might be somewhat unsatisfying.
But, what if we didn't have to cheat at all? We can get the free monoid by tweaking foldMap, and it looks like traverse, so what happens if we do the same manipulation to the latter?
It turns out that lens has a type for this purpose, a slight specialization of which is:
newtype Bazaar a b t =
Bazaar { runBazaar :: forall f. Applicative f => (a -> f b) -> f t }
Using this type, we can reorder traverse to get:
howBizarre :: Traversable t => t a -> Bazaar a b (t b)
howBizarre t = Bazaar $ \k -> traverse k t
But now, what do we do with this? And what even is it? [1]
If we continue drawing on intuition from Foldable, we know that foldMap is related to the free monoid. Traversable has more indexing, and instead of Monoid uses Applicative. But the latter are actually related to the former; Applicatives are monoidal (closed) functors. And it turns out, Bazaar has to do with free Applicatives.
If we want to construct free Applicatives, we can use our universal property encoding trick:
newtype Free p f a =
Free { gratis :: forall g. p g => (forall x. f x -> g x) -> g a }
This is a higher-order version of the free p, where we parameterize over the constraint we want to use to represent structures. So Free Applicative f is the free Applicative over a type constructor f. I'll leave the instances as an exercise.
Since free monoid is a monad, we'd expect Free p to be a monad, too. In this case, it is a McBride style indexed monad, as seen in The Kleisli Arrows of Outrageous Fortune.
type f ~> g = forall x. f x -> g x
embed :: f ~> Free p f
embed fx = Free $ \k -> k fx
translate :: (f ~> g) -> Free p f ~> Free p g
translate tr (Free e) = Free $ \k -> e (k . tr)
collapse :: Free p (Free p f) ~> Free p f
collapse (Free e) = Free $ \k -> e $ \(Free e') -> e' k
That paper explains how these are related to Atkey style indexed monads:
data At key i j where
At :: key -> At key i i
type Atkey m i j a = m (At a j) i
ireturn :: IMonad m => a -> Atkey m i i a
ireturn = ...
ibind :: IMonad m => Atkey m i j a -> (a -> Atkey m j k b) -> Atkey m i k b
ibind = ...
It turns out, Bazaar is exactly the Atkey indexed monad derived from the Free Applicative indexed monad (with some arguments shuffled) [2]:
hence :: Bazaar a b t -> Atkey (Free Applicative) t b a
hence bz = Free $ \tr -> runBazaar bz $ tr . At
forth :: Atkey (Free Applicative) t b a -> Bazaar a b t
forth fa = Bazaar $ \g -> gratis fa $ \(At a) -> g a
imap :: (a -> b) -> Bazaar a i j -> Bazaar b i j
imap f (Bazaar e) = Bazaar $ \k -> e (k . f)
ipure :: a -> Bazaar a i i
ipure x = Bazaar ($ x)
(>>>=) :: Bazaar a j i -> (a -> Bazaar b k j) -> Bazaar b k i
Bazaar e >>>= f = Bazaar $ \k -> e $ \x -> runBazaar (f x) k
(>==>) :: (s -> Bazaar i o t) -> (i -> Bazaar a b o) -> s -> Bazaar a b t
(f >==> g) x = f x >>>= g
As an aside, Bazaar is also an (Atkey) indexed comonad, and the one that characterizes traversals, similar to how indexed store characterizes lenses. A Lens s t a b is equivalent to a coalgebra s -> Store a b t. A traversal is a similar Bazaar coalgebra:
s -> Bazaar a b t
~
s -> forall f. Applicative f => (a -> f b) -> f t
~
forall f. Applicative f => (a -> f b) -> s -> f t
It so happens that Kleisli composition of the Atkey indexed monad above (>==>) is traversal composition.
Anyhow, Bazaar also inherits Applicative structure from Free Applicative:
instance Functor (Bazaar a b) where
fmap f (Bazaar e) = Bazaar $ \k -> fmap f (e k)
instance Applicative (Bazaar a b) where
pure x = Bazaar $ \_ -> pure x
Bazaar ef < *> Bazaar ex = Bazaar $ \k -> ef k < *> ex k
This is actually analogous to the Monoid instance for the free monoid; we just delegate to the underlying structure.
The more exciting thing is that we can fold and traverse over the first argument of Bazaar, just like we can with the free monoid:
bfoldMap :: Monoid m => (a -> m) -> Bazaar a b t -> m
bfoldMap f (Bazaar e) = getConst $ e (Const . f)
newtype Comp g f a = Comp { getComp :: g (f a) } deriving (Functor)
instance (Applicative f, Applicative g) => Applicative (Comp g f) where
pure = Comp . pure . pure
Comp f < *> Comp x = Comp $ liftA2 (< *>) f x
btraverse
:: (Applicative f) => (a -> f a') -> Bazaar a b t -> Bazaar a' b t
btraverse f (Bazaar e) = getComp $ e (c . fmap ipure . f)
This is again analogous to the free monoid code. Comp is the analogue of Ap, and we use ipure in traverse. I mentioned that Bazaar is a comonad:
extract :: Bazaar b b t -> t
extract (Bazaar e) = runIdentity $ e Identity
And now we are finally prepared to not cheat:
honestTraverse
:: (Applicative f, Traversable t) => (a -> f b) -> t a -> f (t b)
honestTraverse f = fmap extract . btraverse f . howBizarre
So, we can traverse by first turning out Traversable into some structure that's kind of like the free monoid, except having to do with Applicative, traverse that, and then pull a result back out. Bazaar retains the information that we're eventually building back the same type of structure, so we don't need any cheating.
To pull this back around to domains, there's nothing about this code to object to if done in a total language. But, if we think about our free Applicative-ish structure, in Haskell, it will naturally allow infinitary expressions composed of the Applicative operations, just like the free monoid will allow infinitary monoid expressions. And this is okay, because some Applicatives can make sense of those, so throwing them away would make the type not free, in the same way that even finite lists are not the free monoid in Haskell. And this, I think, is compelling enough to say that infinite traversals are right for Haskell, just as they are wrong for Agda.
For those who wish to see executable code for all this, I've put a files here and here. The latter also contains some extra goodies at the end that I may talk about in further installments.
[1] Truth be told, I'm not exactly sure.
[2] It turns out, you can generalize Bazaar to have a correspondence for every choice of p
newtype Bizarre p a b t =
Bizarre { bizarre :: forall f. p f => (a -> f b) -> f t }
hence and forth above go through with the more general types. This can be seen here.

 and
and  consists of a pair of functors
consists of a pair of functors 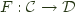 , and
, and 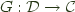 and a natural isomorphism:
and a natural isomorphism: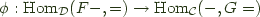
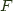 the left adjoint functor, and
the left adjoint functor, and 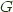 the right adjoint functor and
the right adjoint functor and 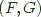 an adjoint pair, and write this relationship as
an adjoint pair, and write this relationship as 
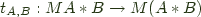
![\bfig \square/>`>`>`>/[F(A)`F(B)`G(A)`G(B);F {[}\hspace{-0.8pt}{[}f, g{]}\hspace{-0.8pt}{]} `\eta_A`\eta_B`G {[}\hspace{-0.8pt}{[}f, g{]}\hspace{-0.8pt}{]}] \efig \bfig \square/>`>`>`>/[F(A)`F(B)`G(A)`G(B);F {[}\hspace{-0.8pt}{[}f, g{]}\hspace{-0.8pt}{]} `\eta_A`\eta_B`G {[}\hspace{-0.8pt}{[}f, g{]}\hspace{-0.8pt}{]}] \efig](http://comonad.com/latex/eb518f091c90f6025d7669a9291b6c29.png)
 Functor that maps everything to
Functor that maps everything to