The Comonad.Reader

No, this isn't some uplifting piece about deriving courage from sloth in the face of adversity.

What I want to talk about is monadic strength.

Transcribing the definition from category theory into Haskell we find that a strong monad is a functor such that there exists a morphism:

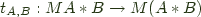
with a couple of conditions on it that I'll get to later.

Currying that to get something that feels more natural to a Haskell programmer we get:

 
mstrength :: Monad m => m a -> b -> m (a,b)
 

Pardo provided us with a nice definition for that in Towards merging recursion and comonads:

 
mstrength ma b = ma >>= (\\a -> return (a,b))
 

which we can rewrite by pulling the return out of the function:

 
mstrength' ma b = ma >>= return . (\\a -> (a,b))
 

Now, one of the nice monad laws we have says that if your Monad is a Functor, which it should be, then:

 
fmap f xs == xs >>= return . f
 

This law is what gives us the definition for liftM modulo the do-sugar used when writing it.

This lets us write:

 
strength :: Functor f => f a -> b -> f (a,b)
strength fa b = fmap (\\a -> (a,b)) fa
 

Then by the monad laws any definition for Monad for this Functor must be strong in the sense that if it was made into a monad, this strength function would be a valid strength for the monad.

So we get the interesting observation that all functors in Haskell are 'strong'. Lets look at a couple:

Example ((,)c)

 
instance Functor ((,)c) where
	fmap f ~(a,b) = (a,f b)
 

The above may be familiar as the reader comonad, or as the functor induced by the (,) Bifunctor.

What is the meaning of its strength?

 
strength{(,)c} :: ((c,a),b) -> (c,(a,b))
 

Well, thats just the associative law for the (,) bifunctor.

Example (Either a)

What about the built-in functor instance for (Either a)?

 
instance Functor (Either a) where
	fmap f (Left a) = Left a
	fmap f (Right b) = Right (f b)
 

 
strength{Either c} :: (Either c a, b) -> Either c (a,b)
 

This strength gives us a (slightly weak) form of distributive law for sums over products in Haskell.

Having strength lets us know that if we have a functor of a's I can go through it and just drop in b's in along side each of the a's.

The show is over. Everyone can go home.

Not quite. What about comonadic costrength?

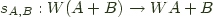
with a couple of laws we can ignore for the moment.

Since we can derive strength for all Functors in Haskell, we'd think at first
that we could do the same for costrength, after all most constructions work out that way when you can
construct one, its dual usually means something interesting and works out fine.

Here I'll introduce a typeclass, foreshadowing that this probably won't go so smoothly:

 
class Functor w => Costrong w where
	costrength :: w (Either a b) -> Either (w a) b
 

Unfortunately costrength cannot be derived for every functor in Haskell. Lets look at what it does and see why.

With costrength, given a data structure decorated at each point with either an 'a' or a 'b' I can walk the entire structure and if I found a's everywhere then I know I have 'a's in every position, so I can strengthen the type to say that it just contains 'a's. Otherwise I found a b, so I'll give you one of the b's I found. This requires that I'm somehow able to decide if the structure contains b's anywhere and constructively give you one if it does.

Lets find a functor that you can't do this to.

 
instance Functor ((->)e) where
         fmap  = (.)
 

An instance of costrength for (->) e,

 
costrength{(->)e} :: (e -> Either a b) -> Either (e -> a) b
 

would be equivalent to deciding that the function returns only Left's for all inputs.

Epic failure; functions are out.

Now, if we restrict ourselves to polynomial functors, we can try again, but what about infinite data structures?

 
data Stream a = a < : Stream a
 

Lets define the following stream comparison function:

 
eqstream :: Eq a => Stream a -> Stream a -> Stream (Either () ())
eqstream (a < : as) (b <: bs) = c <: eqstream as bs where
	c = if a == b then Right () else Left ()
 

Deciding equality of streams is complete , so this would imply that we have an oracle for the halting problem!

Ok, so infinite data structures are out.

This rules out 'coinductive' structures in general, but inductive structures are fine.

So what is in?

In Scheme you can define costrength with a the use of call-cc, which I'll leave as an exercise to the reader.

But, you can't use fmap to do that in Haskell, because call-cc passing around the current continuation is a form of monadic side effect. You could use the old Data.FunctorM and a Cont monad, but we like to think in terms of Data.Traversable today.

Unfortunately 'Either' isn't a Haskell monad in general because of some noise about trying to support 'fail', but if we define a less restrictive Either monad than the one in Control.Monad.Error, like the following:

 
instance Monad (Either a) where
	return = Right
	Left a >>= k = Left a
	Right a >>= k = k a
 

then using the version of mapM in Data.Traversable,

 
mapM :: (Traversable t, Monad m) => (a -> m b) -> t a -> m (t b)
 

if we look at this specialized to 'id',

 
mapM{Either a}  id :: Traversable f => f (Either a b) -> Either a (f b)
 

we have almost has the right type. (In fact the above is probably a more natural signature for costrength in Haskell, because it is a distributive law for any Traversable functor f over (Either a). In fact mapM id (also known as sequence) is a distributive law for a traversable functor over any monad.

If we note the fact that sums are symmetric:

 
class Symmetric p where
     swap :: p a b -> p b a
 
instance Symmetric Either where
    swap (Left a) = Right a
    swap (Right a) = Left a
 

then:

 
costrength :: Traversable f => f (Either a b) = Either (f a) b
costrength = swap . mapM swap
 

The ability to define strength in general came from the fact that we were lazy enough that 'strength' doesn't try to evaluate the potentially infinite structure (there are little hidden functions all over the place in the form of thunks). The trade off is that we aren't 'strict' enough for 'costrength' to be definable in general.

A couple of uses for costrength:

Example (Either c)

 
costrength {Either c} :: Either c (Either a b) = Either (Either c a) b
 

is just the coassociative law for Either.

Example ((,)c)

 
costrength {(,)c} :: (c, Either a b) = Either (c,a) b
 

lets us distribute sums over products another way.

Example []

Finally,

 
costrength {[]} :: [Either a b] -> Either [a] b
 

lets us pretend that we can solve the stream problem above, but it just bottoms out if you apply it to an infinite list.

In short, in Haskell, every Functor is strong and every Traversable Functor is (something like) costrong.

[Edit: Dan Doel pointed out that instead of mapM id you could use sequence]

[Edit: @blaisorblade pointed out that this should really be using traverse these days]

[Edit: This isn't quite costrength. Why? It fails the reverse of the second strength law. In reality we need to limit ourselves further -- to left adjoints.]