First, we can make the generalized hylomorphism from the other day more efficient by noting that once you inline the hylomorphism, you can see that you do 3 fmaps over the same structure, so we can fuse those together yielding:
g_hylo :: (Comonad w, Functor f, Monad m) =>
(forall a. f (w a) -> w (f a)) ->
(forall a. m (f a) -> f (m a)) ->
(f (w b) -> b) ->
(a -> f (m a)) ->
(a -> b)
g_hylo w m f g = extract . g_hylo' w m f g . return
-- | the kernel of the generalized hylomorphism
g_hylo' :: (Comonad w, Functor f, Monad m) =>
(forall a. f (w a) -> w (f a)) ->
(forall a. m (f a) -> f (m a)) ->
(f (w b) -> b) ->
(a -> f (m a)) ->
(m a -> w b)
g_hylo' w m f g =
liftW f . w .
fmap (duplicate . g_hylo' w m f g . join) .
m . liftM g
Also, the above made me realize that most of the generalized cata/ana, etc morphisms give you a little more interesting stuff to do if you separate out the recursive part. Then you can pass it a monad built with something other than return to perform substitution on, or inspect the comonadic wrapper on the result.
Oh, and to support my earlier claim that g_hylo generalizes g_cata and g_ana here are derivations of each in terms of g_hylo.
g_cata :: (Functor f, Comonad w) =>
(forall a. f (w a) -> w (f a)) ->
(f (w a) -> a) ->
Mu f -> a
g_cata k f = g_hylo k (fmap Id . runId) f (fmap Id . outF)
g_ana :: (Functor f, Monad m) =>
(forall a. m (f a) -> f (m a)) ->
(a -> f (m a)) ->
a -> Nu f
g_ana k g = g_hylo (Id . fmap runId) k (InF . fmap runId) g
As an aside, histomorphisms have a dual that seems to be elided from most lists of recursion schemes: Uustalu and Vene call it a futumorphism. It basically lets you return a structure with seeds multiple levels deep rather than have to plumb 'one level at a time' through the anamorphism. While a histomorphism is a generalized catamorphism parameterized by the cofree comonad of your functor, a futumorphism is a generalized anamorphism parameterized by the free monad of your functor.
futu :: Functor f => (a -> f (Free f a)) -> a -> Nu f
futu f = ana ((f ||| id) . runFree) . return
Now, g_hylo is painfully general, so lets look at a particularly interesting choice of comonad and monad for a given functor that always have a distributive law: the cofree comonad, and the free monad of that very same functor!
This gives rise to a particular form of morphism that I haven't seem talked about in literature, which after kicking a few names around on the haskell channel we chose to call a chronomorphism because it subsumes histo- and futu- morphisms.
chrono :: Functor f =>
(f (Cofree f b) -> b) ->
(a -> f (Free f a)) ->
a -> b
Unlike most of the types of these generalized recursion schemes, chrono's type is quite readable!
A chronomorphism's fold operation can 'look back' at the results it has given, and its unfold operation can 'jump forward' by returning seeds nested multiple levels deep. It relies on the fact that you always have a distributive law for the cofree comonad of your functor over the functor itself and also one for the functor over its free monad and so it works for any Functor.
You can generalize it like you generalize histomorphisms and futumorphisms, and derive ana and catamorphisms from it by noting the fact that you can fmap extract or fmap return to deal with the cofree comonad or free monad parts of the term.
Alternately, since the 'identity comonad' can be viewed as the cofree comonad of the  Functor that maps everything to
Functor that maps everything to  , you can also choose to rederive generalized futumorphisms from generalized chronomorphism using the distributive law of the identity comonad.
, you can also choose to rederive generalized futumorphisms from generalized chronomorphism using the distributive law of the identity comonad.
Below you'll find source code for generalized hylo- cata- ana- histo- futu- chrono- etc... morphisms and their separated kernels.
Source Code
As an aside, Dan Doel (dolio) has started packaging these up for addition to category-extras in Hackage.

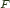 , abide
, abide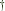 and coabide
and coabide and
and  abide if for all a, b, c, d:
abide if for all a, b, c, d: .
.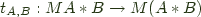
![\bfig \square/>`>`>`>/[F(A)`F(B)`G(A)`G(B);F {[}\hspace{-0.8pt}{[}f, g{]}\hspace{-0.8pt}{]} `\eta_A`\eta_B`G {[}\hspace{-0.8pt}{[}f, g{]}\hspace{-0.8pt}{]}] \efig \bfig \square/>`>`>`>/[F(A)`F(B)`G(A)`G(B);F {[}\hspace{-0.8pt}{[}f, g{]}\hspace{-0.8pt}{]} `\eta_A`\eta_B`G {[}\hspace{-0.8pt}{[}f, g{]}\hspace{-0.8pt}{]}] \efig](http://comonad.com/latex/eb518f091c90f6025d7669a9291b6c29.png)
 Functor that maps everything to
Functor that maps everything to