I have been trying out various representations for higher-order abstract syntax (HOAS) in Haskell, with an eye towards seeing what I can actually use to get real work done and I have run into a few unexpected headaches, and a couple of neat observations. That said, I should probably start by explaining some terminology.

Encoding a language that binds variables in higher order abstract syntax generally involves constructing an abstract data type that contains functions. A functor for representing expressions from Berendregdt's lambda cube in HOAS goes something like (ignoring any consolidation of binders and sorts)

 
data F a
    = Lam a (a -> a)
    | Pi a (a -> a)
    | App a a
    | Star
    | Box
 

There are a number of mathematical functors that are not instances has Haskell's Functor class, such as the above.

If you don't believe me that F is not a functor, try deriving an instance for fmap for F that satisfies the functor laws:

 
fmap id == id
fmap (f . g) == fmap f . fmap g
 

The reason it can't be is that fmap can really only be defined for 'covariant endofunctors on the category of types'.

Most covariant functors used in Haskell are among the so-called 'polynomial' functors, meaning that they can be built up out of sums, products and constants. 

 
data Maybe a = Just a | Nil -- covariant in a
data ListF t a = Cons t a | Nil -- covariant in a
 

That said, polynomial functors are not the only covariant functors, because you can also have some functions in the type, as long as the type over which you are parameterized only occurs in 'positive' position. The informal way to think about it is that every time you have a parameter on the left of an (->) in the type, the occurrence switches signs, starting positive, so for some Functors, you can have functions, as long as the parameter occurs only in positive positions. Most of us know some instances of Functor that are covariant, but not polynomial such as:

 
newtype Reader e a = Reader (e -> a) -- covariant in a
newtype Cont r a = Cont ((a -> r) -> r) -- covariant in a
 

On the other hand the following functors are not covariant, because the parameter occurs in negative position somewhere in the type.

 
data ContravariantSample a = Bar (a -> Int) -- contravariant
data InvariantSample a = Baz (a -> a) -- invariant
 

You could go through and define a 'ContravariantFunctor' type class if you really want:

 
class ContravariantFunctor f where
    cofmap :: (b -> a) -> f a -> f b
 

But for HOAS you tend to need terms like Lam (a -> a) that have both positive and negative occurrences of a to handle variable binding, so we'll skip to a definition for an invariant functor, which we'll choose to call an exponential functor in contrast to a polynomial, because category theory types like to refer to functions as exponentials, and use the notation ba to denote a function of type (a -> b).

 
class ExpFunctor f where
    xmap :: (a -> b) -> (b -> a) -> f a -> f b
 

Now, obviously every Functor is trivially an ExpFunctor, witnessed by the default definition:

 
xmapF :: Functor f => (a -> b) -> (b -> a) -> f a -> f b
xmapF = const . fmap
 

And just as people are wont to do with Functor and Monad you could argue that in an ideal world the definition for Functor should change to class ExpFunctor f => Functor f, but since not that many people use these things, I doubt anyone would be interested in the change.

This is a sufficiently general definition that you can construct instances for exponential data types such as:

 
instance ExpFunctor F where
    xmap f g (Lam t k) = Lam (f t) (f . k . g)
    xmap f g (Pi t k) = Pi (f t) (f . k . g)
    xmap f g (App a b) = App (f a) (f b)
    xmap f g Star = Star
    xmap f g Box = Box
 

As an aside we can define exponential functor composition, just like functor composition if we want to:

 
newtype O f g e = Comp { deComp :: f (g e) }
instance (Functor f, Functor g) => Functor (f `O` g) where
        fmap f = Comp . fmap (fmap f) . deComp
instance (ExpFunctor f, ExpFunctor g) => ExpFunctor (f `O` g) where
        xmap f g = Comp . xmap (xmap f g) (xmap g f) . deComp
 

Typically we'd like to represent the recursive part of a functor with another ADT. This makes it easier to go through and apply things like catamorphisms and anamorphisms to them (see Functional Programming with Bananas, Lenses, Envelopes and Barbed Wire for more information). Catamorphisms are sometimes called bananas because of the notation from that paper.

A typical newtype used for explicit isorecursion is:

 
newtype Nu f  = Nu { old :: f (Nu f) } --so its not funny
 

Now if f is a good old fashioned Functor, we can define a pretty straightforward idea of a catamorphism over Nu f. I want to be able to handle ExpFunctor's later, so we'll leave the Functor constraint off of the class and move it to the instance.

 
class Cata f t | t -> f where
    cata :: (f a -> a) -> t -> a
 
instance Functor f => Cata f (Nu f) where
    cata f = f . fmap (cata f) . old
 

And given cata and fmap one can go through and build up a whole host of other recursion schemes, paramorphisms, zygomorphisms, histomorphisms, generalized catamorphisms, ...; the menagerie is quite forbidding and these can be used to tear apart covariant functors with reckless abandon. With the power of a paramorphism you rederive the notion of general recursion, and so you can basically write any recursive function you want. (On the coalgebra side of the house there are anamorphisms, apomorphisms, and all sorts of other beasts for effectively generating covariant functors)

You can also use them on contravariant functors with some work, because it turns out you can 'square' a contravariant functor to derive a covariant one.

 
newtype Square f a = Square (f (f a))
instance ContravariantFunctor f => Functor (Square f) where
    fmap f = Square . cofmap (cofmap f) . unSquare
 

The problem is that once you weaken from a Functor all the way to an ExpFunctor, most of that machinery goes out the window.

Cue the arrival of Erik Meijer and Graham Hutton. They derived a kind of catamorphism for exponential functors back in 1995 in Bananas in Space.

 
cataMH :: ExpFunctor f => (f a -> a) -> (a -> f a) -> Nu f -> a
cataMH f g = f . xmap (cataMH f g) (anaMH f g) . old
 
anaMH :: ExpFunctor f => (f a -> a) -> (a -> f a) -> a -> Nu f
anaMH f g = Nu . xmap (anaMH f g) (cataMH f g) . g
 

Note the similarity and differences between cataMH and the cata described above. In order to satisfy the type of xmap you need not just an operation to fold your structure, but you need an 'unfold' step as well; to run the catamorphism backwards to satisfy the type of xmap, cataMH requires not just an 'algebra structure' (f a -> a) for folding, but it also requires an inverse 'coalgebra structure' (a -> f a) to unfold what it just did.

In other words, to use the Meijer/Hutton catamorphism to write a pretty printer, you have to write a parser as well; to use it to eval, you must also be able to reify values back into programs.

Unfortunately we won't be able to get an instance of Cata out of the Meijer/Hutton catamorphism.

With it in hand, you can write a pretty powerful HOAS representation, but there are some huge caveats to the Meijer-Hutton catamorphism:

  1. Some catamorphisms don't have inverses!
  2. Since a function in your embedded language is represented as a function in the 'meta-language' Haskell, HOAS functions have the ability to host 'bad terms' that do things that the underlying embedded language can't do like use case to inspect if they were given a lambda or an application as an argument on terms passed to them and do different things accordingly.
  3. Using the inverse can be very slow

Fortunately, a year later Leonidas Fegaras and Tim Sheard realized that the main use of the 'unfold step' above was to just undo the damage caused by the fold step and that a full inverse wasn't needed, just a place holder 'place' such that serves as a right-inverse such that:

 
cata f . place = id
 

The problem the reduces to the question of how to define place. Fegaras and Sheard were willing (and able) to change every functor to include an extra member name Place and then define as part of each catamorphism that cata f (Place x) = x. They then ensured that Place wasn't abused by the programmer by a complicated type system that we really don't have access to in Haskell. So, if you are able to go into some as-yet-unwritten language where their tagged types exist, then your problems are solved for the most part and you can write general recursion over exponential functors without impossible to find inverses, bad terms or expensive inverse operations.

A compromise is to realize as much of the Fegaras/Sheard vision as you can reasonably type in Haskell. As noted by Weirich and Washburn, you can move the 'Place' term into the explicit recursion ADT yielding something like: 

 
data Rec f a = Roll (f (Rec f a)) | Place a
 

This obviates the need to modify every single base functor you use to include a Place term -- admittedly at the cost of introducing another case analysis where a bottom can occur because the recursive data type is no longer a newtype.

We can then readily almost define a catamorphism for this type - ignoring the extra 'a' term in Rec f a for the nonce.

 
cataFS :: ExpFunctor f => (f a -> a) -> Rec f a -> a
cataFS f (Roll x) = f (xmap (cataFS f) Place x)
cataFS f (Place x) = x
 

As an aside to build terms to feed to either of these recursive forms, you need to inject values by wrapping them in the recursive constructor:

 
lamMH :: Nu F -> (Nu F -> Nu F) -> Nu F
lamMH t k = Nu (Lam t k)
 
lamFS :: Rec F a -> (Rec F a -> Rec F a) -> Rec F a
lamFS t k = Roll (Lam t k)
 

You'll note a lot of similarity here, and also a superfluous term 'a' floating around in the Fegaras Sheard definition, which is necessary for Place to work its magic.

Since I want to compare a few different ways to represent HOAS here, lets define:

 
class Rollable f t | t -> f where
    roll :: f t -> t
instance Rollable f (Nu f) where
    roll = Nu
instance Rollable f (Rec f a) where
    roll = Roll
 

Then we can use one function for either recursion scheme that we want to use for our particular functor 'F'.

 
lam :: Rollable F t => t -> (t -> t) -> t
lam t f = roll (Lam t f)
 
app :: Rollable F t => t -> t -> t
app f a = roll (App f a)
 
...
 

The problem then comes down to the fact that when working with the Fegaras/Sheard form, you have a superfluous term 'a' that can bite you when you go to apply two different catamorphisms to your HOAS term. The first will fix your type to the return type of its catamorphism and you'll be done for when you attempt to apply a different catamorphism that needs a different type.

One fix, as noted by Washburn and Weirich is to quantify over the a with an explicit forall when working with the Fegaras/Sheard catamorphism. This has the nice side effect that it prevents illegal uses of 'Place'. Moreover, that explicit quantifier allows you to use different catamorphisms over the term.

So, now instead of being interested in terms of the type 'Rec f a' we want terms of the type 'forall a. Rec f a', but then we run into another problem!

You can't define a typeclass instance for a type that has a leading explicit 'forall' quantifier, and I for one really like to be able to use typeclasses like Show, Eq, etc over my types.

However, Shae Erisson and I noticed the fact that you can define the following strange, beautiful but legal newtype to box up the quantifier:

 
newtype ForAll f = ForAll { runForAll :: forall a. f a }
 

This lets us define a better catamorphism which doesn't suffer from the monomorphism problems that the previous version did, and finally we get an instance of Cata for the FegarasSheard catamorphism.

 
 
instance ExpFunctor f => Cata f (ForAll (Rec f)) where
    cata f = cataFS f . runForAll
 

A lambda calculus pretty printer in the style of Washburn and Weirich's Boxes Go Bananas goes something like the following (although you need -fallow-undecidable-instances in GHC.

 
instance Cata F (ForAll t) => Show (ForAll t) where
    show x = cata phi x vars where
        phi (Lam t k) (v:vars) =
            "(\\\\" ++ v ++ ": " + t vars ++ ". " ++ k (const v) vars ++ ")"
	phi (App a b) vars =
            "(" ++ a vars ++ " " ++ b vars ++ ")"
        ...
	vars =
            [ [i] | i < - ['a'..'z']] ++
            [i : show j | j <- [1..], i <- ['a'..'z'] ]
 

All is not roses, however. We still haven't ruled out bad functions that inspect the functor they are given.

Washburn and Weirich go off and change the form of the recursion data type yet again to yield an explicit elimination form with some benefits and costs, which I can represent here as:

 
type Rec' f a = (f a -> a) -> a
 

As an interesting aside, you may notice some similarities to the type of the continuation monad:

 
newtype Cont r a = Cont ((a -> r) -> r)
 
 
type Rec'' w a = Cont a (w a)
 

I'll have more to say about this curious use of a monad later on, but unfortunately Rec and Rec'' can't be used with ForAll as they stand, so we have to introduce yet another newtype so that they can be partially applied -- thankfully these are free at runtime!

 
newtype Elim f a = Elim { unElim :: Cont a (f a) }
elim = Elim . Cont
runElim = runCont . unElim
 

Now, we can define the relevant typeclasses needed to support all the Fegaras and Sheard machinery for this type:

 
instance ExpFunctor f => Rollable f (Elim f a) where
    roll x = elim $ \f -> f $ xmap (cata f) place x
 
instance Placeable Elim where
    place = elim . const
 
instance Cata f (ForAll (Elim f)) where
    cata f x = runElim (runForAll x) f
 

After all of that, we basically get the 'iteration library interface' of Boxes Go Bananas packaged up so that we can play with these representations more or less interchangeably.

Now for the problem.

Weirich and Washburn's encoding as an elimination form protect the user from bad case analysis by denying you the ability to inspect terms with case at all. This is immediately apparent by the signature of Rec' f a above:

In their encoding:

 
cata x f = f x
 

In other words, the only thing you can do to a term is apply a catamorphism to it. They even say as much somewhere in the paper.

No sweat, we can go rederive all of the other stuff thats defined in terms of catamorphism, right? paramorphisms, zygomorphisms, histomorphisms, generalized catamorphisms, and then we can do anything we want, right? Unfortunately, here is where we run out of steam.

A catamorphism isn't strong enough to encode general recursion without fmap. In order to rederive general recursion from a catamorphism you need at least a paramorphism. Normally we can define a paramorphism in terms of our catamorphism with the use of fmap, but as we are working over merely an exponential functor we do not have fmap!

I ran headlong into this wall, while trying to derive a minimalist dependently-typed lambda calculus implementation using the Boxes Go Bananas encoding, because typechecking requires normal form reduction, which could be cleanly encoded as a paramorphism, but which couldn't seem to be represented in the Boxes Go Bananas style.

Depending on how bad we want to be, we can get out of the Washburn/Weirich or Fegaras/Sheard sandboxes and into one of the others. Though curiously we can't get back out of the Meijer/Hutton-style unless we have a full Functor.

 
 
reroll :: (Cata f t, Rollable f t') => t -> t'
reroll = cata roll
 
-- | safe $$ hoas-expression
safe :: (forall a. Elim f a) -> ForAll (Elim f)
safe = ForAll
 
-- | unsafe $$ hoas-expression
unsafe :: (forall a. Rec f a) -> ForAll (Rec f)
unsafe = ForAll
 
-- | cast to Meijer/Hutton
toMH :: (Cata f t, Functor f) => t -> Nu f
toMH = cata Nu
 
-- | cast to Washburn/Weirich
toWW :: (Cata f t, ExpFunctor f) => t -> ForAll (Elim f)
toWW x = ForAll (reroll x)
 
-- | cast to Fegaras/Sheard
toFS :: (Cata f t, ExpFunctor f) => t -> ForAll (Rec f)
toFS x = ForAll (reroll x)
 

It seems we can get to a point where the System 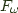F_\omega fragment of Haskell protects us from ourselves, preventing bad case analysis and abuse of the place term, but in the process we give up general recursion.

For now, I think I have to hop out to at least the Fegaras and Sheard encoding to get any work done.

Source Code