The Comonad.Reader

Recently Eric Kidd and Dan Piponi have used a bit of type hackery by Oleg Kiselyov and -fno-implicit-prelude to build some interesting restricted monads, like the Wadler Set and Bag monads.

There is another interesting monad variation - a parameterized monad - where the monad carries around an additional parameter at the type level such as a type-level set of effects. One really good example of this is the separation logic monad in Hoare Type Theory. The pre- and post- conditions can be viewed as the parameter carried around on that monad. Wadler and Thiemann, Jean-Christophe Filliâtre and others have explore this notion for encoding effects.

This prompts the question of if parameterized monads can be implemented directly in Haskell. Indeed they can, but a simple version fails with the signature:


class BadHaskell m p p' p'' | p p' -> p'' where
return :: a -> m p a
fail :: a -> m p a
(>>=) :: m p a -> (a -> m p' a) -> m p'' a


This of course runs afoul of the fact that all of the parameters are not mentioned in return, so we have to break it apart into two or three classes.


class Return m p where
return :: a -> m p a

class Fail m p where
fail :: String -> m p a

class Bind m p p' p'' | p p' -> p'' where
(>>=) :: m p a -> (a -> m p' a) -> m p'' a


By splitting off fail, we can make it so that it is illegal to use an incomplete pattern on certain monads, a small win, but it may be useful in a later post.

However, there turns out to be quite some awkwardness from the perspective of type inference with this type. In particular we are used to the types of our monads being able to be inferred from the type of their results, but we lose this inference on return. Moreover, we can't just use existing monads under this syntax, we'd have to lift them into a newtype that accepted the additional parameter.

Ignoring the problems with existing monads, and correcting the type inference problem directly by adding fundeps doesn't help as


class Bind m p p' p''
| p -> p' p''
, p' -> p p''
, p'' -> p p'
where
(>>=) :: m p a -> (a -> m p' a) -> m p'' a


is too restrictive and could be shown that under a strict interpretation of the laws, would never be able to be made to satisfy the monad laws except in the base case, because of the inability to construct an associative operation combining the parameters that isn't trivial.

As an aside, speaking of failing monad laws, it is interesting to note that the Set restricted monad actually fails a monad law given that functions in haskell need not respect equality, since fails to hold in general for user defined equality as used by the Set monad, as noted by Andrea Vezzosi on #haskell, the order of association can make a difference as to the result of the computation. This is arguably a minor quibble as you wouldn't be using it unless you knew the type you were going to pass around and how your functions worked on it with respect to its notion of equality.

Turning back to the issue of being unable to pass traditional monads into this type, we realize that having a separate m and p parameters to the type class is redundant as you can generate an equivalent notion by letting m vary.


class Return m where
return :: a -> m a

class Fail m where
fail :: String -> m a

class Bind m m' m'' | m m' -> m'' where
(>>=) :: m a -> (a -> m' a) -> m'' a


This still has the problem that the type of return is not inferable, but now at least we can derive instances of these classes for instances of Monad. Of course, if we create a generic instance for


import qualified Control.Monad as Old
instance Old.Monad m => Bind m m m where (>>=) = (Old.>>=)
...


we then run afoul of the fact that we can't define any other interesting instances because the compiler won't know which way to go with type class inference.

However, even without that we can import each monad in turn, and define some interesting interfaces between them:


instance Bind Maybe [] [] where
Just a >>= f = f a
Nothing >>= _ = []

-- testMaybeList :: [Int] = [2,4]
testMaybeList = Just 2 >>= \x -> [x*1,x*2]


Admittedly there is an 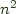combinatorial explosion of combinations and not all of them have clear semantics, but we can choose to implement only the ones that have an unambiguous interpretation and leave off the rest and pay as we go, implementing them as needed. A more mature version of this might provide an interesting alternative/supplement to the MTL approach and can be viewed as a limited fragment of Lüth and Ghani's monad composition through coproducts.

However, we still haven't solved the return problem, but it turns out that monad laws can come to the rescue.

If we start to implement a number of these we notice a pattern when it comes to the Identity monad. In general we can define instances of Bind for the Identity monad for any monad presuming we can liftM, to handle the case on the right, but since liftM requires a sort of circular dependency loop, we choose to make Bind enforce the availability of fmap, allow overlapping instances, and then define:


class (Functor m, Functor m', Functor m'') => Bind m m' m''
| m m' -> m''
where
(>>=) :: m a -> (a -> m' b) -> (m'' b)
(>>) :: m a -> m' b -> m'' b
m >> k = m >>= const k

instance Functor a => Bind Identity a a where
m >>= f = f (runIdentity m)

instance Functor a => Bind a Identity a where
m >>= f = fmap (runIdentity . f) m

-- and to disambiguate between the above instances...
instance Bind Identity Identity Identity where
m >>= f = f (runIdentity m)


The correctness of this is in fact enforced by the monad laws as these instances can be read as the familiar laws once you remove the noise of the Identity monad:


return m >>= f = f m
m >>= return . f = fmap f m
return m >>= f = f m


This gives us a single natural notion of return for all monads that we can use and still glue together via >>=:


class Return m where
returnM :: a -> m a

return :: a -> Identity a
return = Old.return


Now the problem is if you write a statement like return 2 >>= \x -> return (x+1), you can have the Identity type percolate out of your monad expression, even when you were expecting a ListT or State monad or something more interesting, so we need a way to transform values from the Identity monad to an arbitrary monad for use when you want its type to conform to an external signature.


class Go n m where
go :: n a -> m a

instance Return a => Go Identity a where
go = returnM . runIdentity
instance Go a a where
go = id


So, now we can tell our code to go (do something) and it will transform any lingering Identities to whatever monadic type is inferred for the go statement in its current context.

This has the advantage that pure fragments in our monadic sugar can avoid carrying around the rest of the monadic plumbing, even though they use the same bind operator to string it all together.

We can perform similar surgery on the MonadPlus class, tearing it apart into two pieces, breaking out a canonical mzero implementation as a trivial monad that just projects everything to bottom, and having Go erase any lingering mzeros that percolate out of our expression. Rather than reproduce it here, I point to a darcs repository that I just created. You can use darcs to get http://comonad/com/haskell/monad-param or pull the package from hackage. The interesting bits are in Control.Monad.Parameterized and HTML documentation is available.

This package re-exports the MTL and STM monads to avoid the requirement that the end user explicitly import Control.Monad.* masking off the members of Control.Monad each time and it provides some interesting mixins.

Caveat: It appears that GHC enforces the fact that the arguments and results of (>>=) must have a signature like

(>>=) :: forall m a. (...) => m a -> (a -> m b) -> m b

insofar as when you use the do-sugar, your types will not be able to vary. Ideally it should be able to get by with a more liberal signature, but it seems like no one has needed it before now.