Just Fokkinga Abide

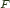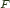I did some digging and found the universal operations mentioned in the last couple of posts: unzip, unbizip and counzip were referenced as abide ${}_F$ , abide ${}_\dagger$ and coabide ${}_F$ -- actually, I was looking for something else, and this fell into my lap.

They were apparently named for a notion defined by Richard Bird back in:

R.S. Bird. Lecture notes on constructive functional programming. In M. Broy, editor, Constructive Methods in Computing Science. International Summer School directed by F.L. Bauer [et al.], Springer Verlag, 1989. NATO Advanced Science Institute Series (Series F: Computer and System Sciences Vol. 55).

The notion can be summed up by defining that two binary operations $\mathbin{\htmlClass{vertical-operator}{\ominus}}$ and $\ominus$ abide if for all a, b, c, d:

$(a \ominus b) \mathbin{\htmlClass{vertical-operator}{\ominus}} (c \ominus d) = (a \mathbin{\htmlClass{vertical-operator}{\ominus}} c) \ominus (b \mathbin{\htmlClass{vertical-operator}{\ominus}} d)$ .

There is a cute pictorial explanation of this idea in Maarten Fokkinga's remarkably readable Ph.D dissertation on p. 20.

The idea appears again on p.88 as part of the famous 'banana split' theorem, and then later on p90 the above names above are given along with the laws:

fmap f &&& fmap g = unfzip . fmap (f &&& g)
bimap f g &&& bimap h j = unbizip . bimap (f &&& h) (g &&& j)
fmap f ||| fmap g = fmap (f ||| g) . counfzip

That said the cases when the inverse operations exist do not appear to be mentioned in these sources.

Discussion

pozorvlakMay 9th, 2008 at 8:25 am

It’s worth mentioning that if two abiding operations have identities, then they’re equal to each other and commutative, and the identities coincide.

Let + and * be abiding binary operations, with identities 0 and * respectively. Then

0 = 0+0 = (0*1)+(1*0) = (0+1)*(1+0) = 1*1 = 1

And now:

x*y = (0+x)*(y+0) = (0*y)+(x*0) = (1*y)+(x*1) = y+x = (y*1)+(1*x) = (y+1)*(1+x) = (y+0)*(0+x) = y*x = (0+y)*(x+0) = (0*x)+(y*0) = (1*x)+(y*1) = x+y

This is the Eckmann-Hilton argument beloved of category theorists: among its implications are that a monoid object in the category of monoids is a commutative monoid, and that all higher homotopy groups are abelian. It becomes particularly elegant when you use the

x | y =(x*y)+(y*w)
z | w

notation – try it! The proof can be written in a circle, and it’s then called the Eckmann-Hilton clock.

The Catsters have done a video about the Eckmann-Hilton argument.

pozorvlakMay 9th, 2008 at 10:08 am

OK, that’s totally weird. You seem to have blocked the comment in which I explained the connection to the Eckmann-Hilton argument, and let through my two subsequent comments (in which I tried to reproduce the proof in all its 2-dimensional glory, and in which I complained that my <pre> tags had been stripped, rendering the proof unintelligible).

So, for those who are feeling confused: if * and + abide and have units 1 and 0, then 0=1, *=+, and * (and hence +) is commutative. The proof’s fun and reasonably straightforward, particularly if you use the 2-d notation. This is known as the Eckmann-Hilton argument, and it’s famous in category theory, having many beautiful consequences.

Edward KmettMay 9th, 2008 at 10:43 am

I assure you there was no malice in the filtering, it was done automatically because of the link.

Fixed!

Great catch regarding the Eckmann-Hilton bit. Encoding it into Haskell for bifunctors as we speak. =)

pozorvlakMay 9th, 2008 at 2:05 pm

Ah, right, that explains it.

I’ve blogged the 2-d version of the proof here: I think you’ll like it. I look forward to seeing your code!