Thu 5 Jun 2008
I've had a few people ask me questions about Adjunctions since my recent post and a request for some more introductory material, so I figured I would take a couple of short posts to tie Adjunctions to some other concepts.
Representable Functors
A covariant functor 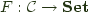 is said to be representable by an object
is said to be representable by an object  if it is naturally isomorphic to
if it is naturally isomorphic to 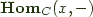 .
.
We can translate that into Haskell, letting  play the role of
play the role of  with:
with:
class Functor f => Representable f x where rep :: (x -> a) -> f a unrep :: f a -> (x -> a) {-# RULES "rep/unrep" rep . unrep = id "unrep/rep" unrep . rep = id #-}
It is trivial to show that any two representations of a given functor must be isomorphic, and that there is a natural isomorphism between any two functors with the same representation, so we could strengthen the signature of the type class above by adding a pair of functional dependencies: f -> x, x -> f, but lets work without this straightjacket for now.
Example
We can represent the anonymous reader monad with its environment.
instance Representable ((->)x) x where rep = id unrep = id
Example
We could adopt the pleasant fiction that () has a single inhabitant to avoid bringing in an empty type, but lets do this correctly. Clearly the Identity functor needs no extra information from its representation.
data Void {- you'll need EmptyDataDecls -} instance Representable Identity Void where rep f = Identity (f undefined) unrep = const . runIdentity
Adjunctions
If you recall the definition of Adjunctions over  from before:
from before:
class (Functor f, Functor g) => Adjunction f g | f -> g, g -> f where unit :: a -> g (f a) counit :: f (g a) -> a leftAdjunct :: (f a -> b) -> a -> g b rightAdjunct :: (a -> g b) -> f a -> b unit = leftAdjunct id counit = rightAdjunct id leftAdjunct f = fmap f . unit rightAdjunct f = counit . fmap f
We can generate a lot of representable functors, by turning to the theorem mentioned in the Wikipedia article about the representability of a right adjoint in terms of its left adjoint wrapped around a singleton element:
Any functor
with a left adjoint
is represented by (FX, ηX(•)) where X = {•} is a singleton set and η is the unit of the adjunction.
Well, earlier we defined a singleton set, Void, and  can play the role of
can play the role of  as we did above. For
as we did above. For 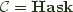 , we can translate the remainder quite easily:
, we can translate the remainder quite easily:
repAdjunction :: Adjunction f g => (f Void -> a) -> g a repAdjunction f = leftAdjunct f undefined unrepAdjunction :: Adjunction f g => g a -> (f Void -> a) unrepAdjunction = rightAdjunct . const
Now, as usual the way type class inference works in Haskell requires us to reason somewhat backwards.
You'd like to say:
instance Adjunction f g => Representable g (f Void) where rep = repAdjunction; unrep = unrepAdjunction
But if you do so, you can't define any other instances for Representable, you'll have used up the instance head, so the previous definitions couldn't be made.
On the other hand, you can create the obligation for an appropriate instance of Representable by changing the signature of Adjunction:
class (Representable g (f Void), Functor f) => Adjunction f g | f -> g, g -> f where ...
Then the definitions for repAdjunction and unrepAdjunction can be used by any would-be Adjunction to automatically generate the corresponding Representable instance, just like liftM can alwyas be used to make a Haskell Monad into a Functor.
We can also go the other way and define an Adjunction given a representation for the right adjoint, but I'll leave that as an exercise for the reader. (Hint: you'll probably want to weaken the signature for Adjunction to remove the fundeps, so you can test some simple cases). You may also want to take a look at the section on Adjunctions as Kan extensions portion of the earlier post.
I have since modified category-extras definition of Adjunction to require the instance for Representable motivated above.
Haddock:
[Control.Functor.Adjunction]
[Control.Functor.Representable]

June 5th, 2008 at 3:34 pm
[...] Now, we would like to do the same thing we did with Representable last time, and just require the user of the Adjunction class to provide us with more instances, something like: [...]
June 13th, 2008 at 5:33 pm
Just to let you know that this post helped my understanding of category-theoretic representability and representable functors.
September 23rd, 2022 at 3:20 am
Viagra tablets https://500px.com/p/skulogovid/?view=groups...
You made your point very clearly…..
September 24th, 2022 at 12:29 am
northwest pharmacies https://reallygoodemails.com/canadianpharmaceuticalsonlineusa...
Whoa lots of beneficial tips!…
September 24th, 2022 at 4:10 am
Viagra from canada https://www.provenexpert.com/canadian-pharmaceuticals-online-usa/...
Terrific content, Thanks a lot!…
September 24th, 2022 at 9:17 am
5 mg viagra coupon printable https://sanangelolive.com/members/pharmaceuticals...
Nicely put, Thanks!…
September 26th, 2022 at 8:10 am
Viagra generico https://melaninterest.com/user/canadian-pharmaceuticals-online/?view=likes...
You explained this really well….
September 26th, 2022 at 12:13 pm
Viagra generic https://haikudeck.com/canadian-pharmaceuticals-online-personal-presentation-827506e003...
You made your stand pretty nicely!!…
September 26th, 2022 at 4:23 pm
online pharmacies canada https://buyersguide.americanbar.org/profile/420642/0...
You actually revealed this perfectly!…
September 27th, 2022 at 12:05 am
Viagra for daily use https://experiment.com/users/canadianpharmacy...
You’ve made your stand very nicely!….
September 27th, 2022 at 6:03 am
Viagra lowest price https://slides.com/canadianpharmaceuticalsonline...
Whoa quite a lot of useful info….
September 27th, 2022 at 9:40 am
stromectol buy https://challonge.com/esapenti...
Cheers, A good amount of write ups!
…
September 27th, 2022 at 2:09 pm
Viagra dosage https://challonge.com/gotsembpertvil...
Awesome data, Kudos….
September 28th, 2022 at 3:56 am
Viagra sans ordonnance https://challonge.com/citlitigolf...
You mentioned this perfectly!…
September 28th, 2022 at 7:30 am
Buy viagra https://order-stromectol-over-the-counter.estranky.cz/clanky/order-stromectol-over-the-counter.html...
Useful knowledge. Many thanks!…
September 28th, 2022 at 1:57 pm
stromectol online https://soncheebarxu.estranky.cz/clanky/stromectol-for-head-lice.html...
This is nicely said! ….
September 29th, 2022 at 3:29 am
purchase stromectol https://lehyriwor.estranky.sk/clanky/stromectol-cream.html...
Fine data. Thanks a lot….
September 29th, 2022 at 7:16 am
Viagra lowest price https://dsdgbvda.zombeek.cz/...
Information clearly considered…..
September 29th, 2022 at 1:42 pm
stromectol cream https://inflavnena.zombeek.cz/...
You said this adequately!…
September 30th, 2022 at 7:59 am
Viagra daily https://www.myscrsdirectory.com/profile/421708/0...
Kudos. Ample data.
…
September 30th, 2022 at 3:08 pm
5 mg viagra coupon printable https://supplier.ihrsa.org/profile/421717/0...
You definitely made your point!…
October 1st, 2022 at 5:31 am
Low cost viagra 20mg https://wefbuyersguide.wef.org/profile/421914/0...
Very good information. Cheers….
October 1st, 2022 at 9:31 am
northwestpharmacy https://legalmarketplace.alanet.org/profile/421920/0...
Regards, Valuable information….
October 2nd, 2022 at 3:08 am
Viagra generic https://moaamein.nacda.com/profile/422018/0...
You mentioned it well!…
October 2nd, 2022 at 7:35 am
canadian pharmacy online https://www.audiologysolutionsnetwork.org/profile/422019/0...
Thanks a lot! I value this….
October 2nd, 2022 at 10:53 am
Cheap viagra https://network.myscrs.org/profile/422020/0...
Reliable stuff. With thanks….
October 3rd, 2022 at 4:38 am
Canadian viagra https://sanangelolive.com/members/canadianpharmaceuticalsonlineusa...
Valuable write ups. Kudos….
October 3rd, 2022 at 8:02 am
ivermectin dosage https://sanangelolive.com/members/girsagerea...
Cheers. Fantastic stuff….
October 4th, 2022 at 6:42 am
Viagra generika https://www.ecosia.org/search?q=“My Canadian Pharmacy – Extensive Assortment of Medications – 2022″…
Superb advice. Cheers….
October 4th, 2022 at 10:25 am
Viagra canada https://www.mojomarketplace.com/user/Canadianpharmaceuticalsonline-EkugcJDMYH...
You actually suggested that fantastically!…
October 4th, 2022 at 2:50 pm
Viagra cost https://seedandspark.com/user/canadian-pharmaceuticals-online...
Cheers. I value it!…
October 5th, 2022 at 2:44 am
Interactions for viagra https://www.giantbomb.com/profile/canadapharmacy/blog/canadian-pharmaceuticals-online/265652/...
Really loads of useful tips….
October 5th, 2022 at 11:43 am
Generic for viagra https://feeds.feedburner.com/bing/Canadian-pharmaceuticals-online...
Factor well applied!!…
October 5th, 2022 at 4:33 pm
Viagra for sale https://search.gmx.com/web/result?q=“My Canadian Pharmacy – Extensive Assortment of Medications – 2022″…
You mentioned it wonderfully!…
October 6th, 2022 at 1:40 am
canadian pharmacies online prescriptions https://search.seznam.cz/?q=“My Canadian Pharmacy – Extensive Assortment of Medications – 2022″…
Thank you! A lot of info!
…
October 6th, 2022 at 5:20 am
Viagra sans ordonnance https://sanangelolive.com/members/unsafiri...
Lovely data. Thanks….
October 6th, 2022 at 9:38 am
Viagra great britain …
Fantastic forum posts. Many thanks!…
October 6th, 2022 at 3:36 pm
Viagra lowest price https://swisscows.com/en/web?query=“My Canadian Pharmacy – Extensive Assortment of Medications – 2022″…
Factor nicely utilized!….
October 7th, 2022 at 2:50 am
Tadalafil https://www.dogpile.com/serp?q=“My Canadian Pharmacy – Extensive Assortment of Medications – 2022″…
Nicely expressed truly. ….
October 7th, 2022 at 9:58 am
Viagra vs viagra …
Fine postings. Appreciate it….
October 8th, 2022 at 5:58 am
Viagra generique https://search.givewater.com/serp?q=“My Canadian Pharmacy – Extensive Assortment of Medications – 2022″…
Thank you. Loads of postings!
…
October 8th, 2022 at 11:26 am
Viagra generico https://www.bakespace.com/members/profile/Сanadian pharmaceuticals for usa sales/1541108/…
Many thanks, Numerous postings!
…
October 9th, 2022 at 4:34 am
canadian pharmacy king …
Appreciate it, Numerous postings!
…
October 9th, 2022 at 9:43 am
Viagra 5mg prix https://results.excite.com/serp?q=“My Canadian Pharmacy – Extensive Assortment of Medications – 2022″…
You expressed that really well….
October 9th, 2022 at 2:12 pm
canadian pharmacy uk delivery https://www.infospace.com/serp?q=“My Canadian Pharmacy – Extensive Assortment of Medications – 2022″…
Whoa loads of useful advice!…
October 10th, 2022 at 6:27 am
canadian pharmaceuticals online https://headwayapp.co/canadianppharmacy-changelog...
This is nicely put! ….
October 11th, 2022 at 4:23 am
Viagra tablets australia https://results.excite.com/serp?q=“My Canadian Pharmacy – Extensive Assortment of Medications – 2022″…
You actually mentioned this exceptionally well….
October 13th, 2022 at 11:42 am
Generic viagra https://feeds.feedburner.com/bing/stromectolnoprescription...
You have made your point pretty effectively!….
October 14th, 2022 at 4:14 am
canada viagra https://reallygoodemails.com/orderstromectoloverthecounterusa...
Good posts. Thank you!…